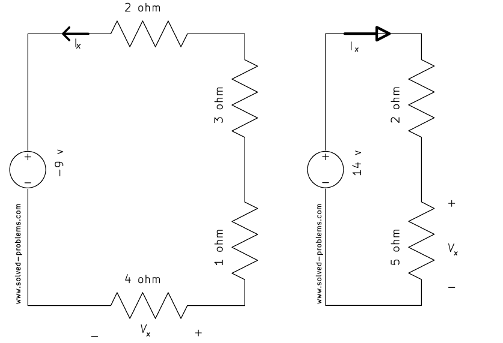
Find ![]() (or
(or ![]() ) and
) and ![]() (or
(or ![]() ) using voltage division rule.
) using voltage division rule.
a)

b)

c)

d)

Solution
a)

Voltage divider: ![]()
Ohm’s law: ![]()
b)

Voltage divider: ![]()
Ohm’s law: ![]()
Please note that ![]() is leaving from the positive terminal of
is leaving from the positive terminal of ![]() . Therefore, applying the Ohm’s law results in
. Therefore, applying the Ohm’s law results in ![]() .
.
c)

Voltage divider: ![]()
Ohm’s law: ![]()
d)

The tricky part in this problem is the polarity of ![]() . In the defined formula for voltage divider, the current is leaving the voltage source from the positive terminal and entering to resistors from positive terminals. In this problem, the current is entering to the the resistor from the negative terminal. Therefore, the voltage for
. In the defined formula for voltage divider, the current is leaving the voltage source from the positive terminal and entering to resistors from positive terminals. In this problem, the current is entering to the the resistor from the negative terminal. Therefore, the voltage for ![]() is the negative of the voltage obtained from the voltage divider formula. The reason is that another voltage can be defined with the inverse polarity and its value can be found using the voltage division rule.
is the negative of the voltage obtained from the voltage divider formula. The reason is that another voltage can be defined with the inverse polarity and its value can be found using the voltage division rule. ![]() is the negative of the defined voltage because it represents the voltage across the same nodes with inverse polarity.
is the negative of the defined voltage because it represents the voltage across the same nodes with inverse polarity.
Voltage divider: ![]()
Ohm’s law (![]() is entering from the negative terminal of
is entering from the negative terminal of ![]() ):
): ![]()
.
it is good
Please correct the answers for question d) on your Problem 1-16: Voltage Divider page.
The web address is: http://www.solved-problems.com/circuits/electrical-circuits-problems/494/voltage-divider/
I believe the Vx = -7.143V and Ix = 1.429A
Done. Thanks
Wyer-transformation
Thank you, these are very useful.