Use nodal analysis method to solve the circuit and find the power of the ![]() – resistor.
– resistor.
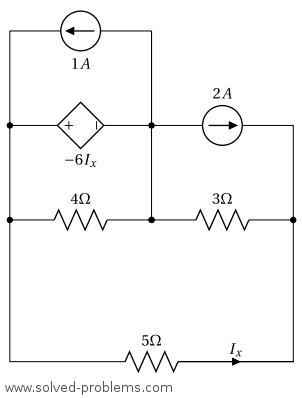
Solution
I. Identify all nodes in the circuit.
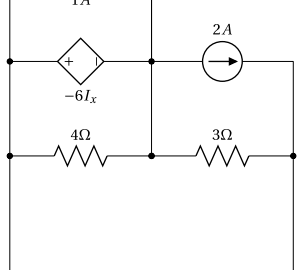
The circuit has 3 nodes as shown below.
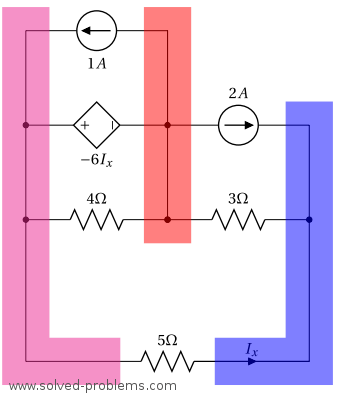
II. Select a reference node. Label it with the reference (ground) symbol.
The node in the middle is connected to 5 nodes and is the node with the largest number of elements connected to it. Therefore, we select it as the reference node of the circuit.
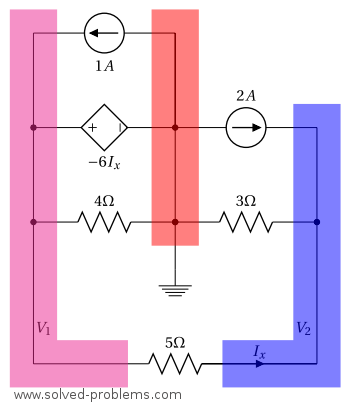
III. Assign a variable for each node whose voltage is unknown.
We label the remaining nodes as shown below. ![]() is connected to the reference node through a voltage source. Therefore, it is equal to the voltage of the dependent voltage source:
is connected to the reference node through a voltage source. Therefore, it is equal to the voltage of the dependent voltage source: ![]() .
.
IV. If there are dependent sources in the circuit, write down equations that express their values in terms of node voltages.
The voltage of the dependent voltage source is ![]() . We should find this value in terms of the node voltages.
. We should find this value in terms of the node voltages. ![]() is the current of the
is the current of the ![]() – resistor. The voltage across the resistor is
– resistor. The voltage across the resistor is ![]() . You may ask why not
. You may ask why not ![]() . Well, that is also correct; the voltage across the resistor is either
. Well, that is also correct; the voltage across the resistor is either ![]() or
or ![]() depend on which terminal we choose to be the positive one. In this circuit, we are going to use this voltage drop to determine
depend on which terminal we choose to be the positive one. In this circuit, we are going to use this voltage drop to determine ![]() . We prefer to use
. We prefer to use ![]() simply because
simply because ![]() is the voltage of the terminal that
is the voltage of the terminal that ![]() entering from. Therefore, the Ohm’s law can be applied in the simple form of
entering from. Therefore, the Ohm’s law can be applied in the simple form of ![]() . By using the voltage drop
. By using the voltage drop ![]() , we have
, we have ![]()
V. Write down a KCL equation for each node.
Node of ![]() :
:
Because there is a voltage source in this node, there is no advantage in writing a KCL equation for this node. All we need to do is to use the voltage of the dependent voltage source and its relation with other node voltages:
![]()
Node of ![]() :
:
![]()
Substituting ![]() ,
,
![]()
All node voltages are obtained. The power of the ![]() -resistor is
-resistor is
![]()
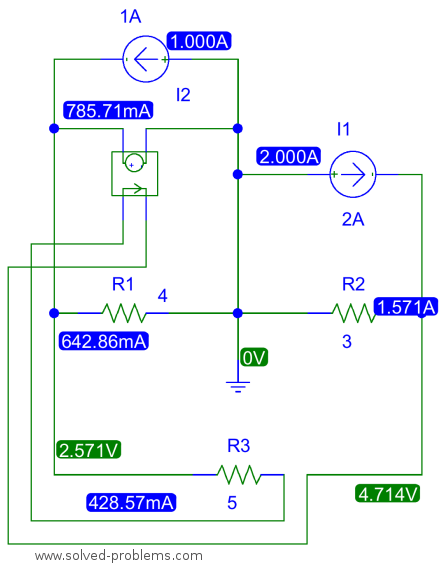
The PSpice simulation result is illustrated below. The PSpice schematics can be downloaded from http://www.solved-problems.com/download/1-21.zip.
Thanks for the post. Very helpful.
thanx alot but i need Pspise simulation file <<and i cant download it <<
thank you very much, it was helpful on the dependent source part of the circuit.