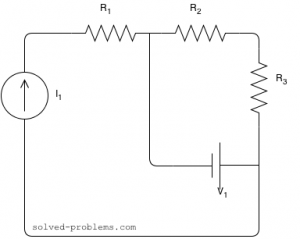
Find the voltage across the current source and the current passing through the voltage source.
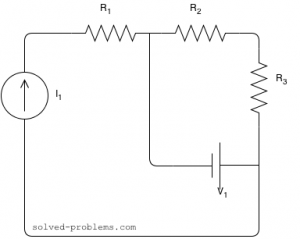
Assume that ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,
Solution
![]() is in series with the current source; therefore, the same current passing through it as the current source:
is in series with the current source; therefore, the same current passing through it as the current source:
![]()
and the voltage across ![]() can be found by Ohm’s law:
can be found by Ohm’s law:
![]()
To find the voltage across the current source, KVL can be applied around the left hand side loop:
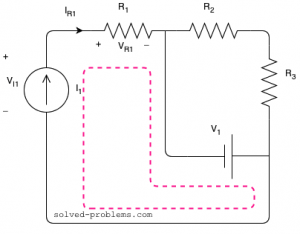
The direction does not matter and would not change the result.
![]()
![]() .
.
![]() and
and ![]() are also in series and their equivalent is
are also in series and their equivalent is ![]()
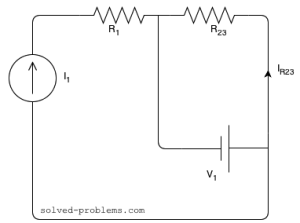
![]() is parallel with the voltage source. This means that its voltage is equal to the voltage of the voltage source.
is parallel with the voltage source. This means that its voltage is equal to the voltage of the voltage source.
![]()
Now, using the Ohm’s law, the current passing through ![]() can be calculated:
can be calculated:
![]()
To find the current of the voltage source, we can apply KCL at one of the nodes:
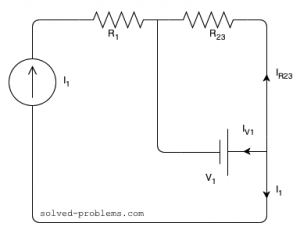
![]()
![]()
Now, you tell me below what the power of each sources are?
plz solve exercise problems on Nortons theorem from BE 3 Sem na books
Have you checked out ?
And let me know which problem you would like me to solve.
i will need some kvl&kcl simple problem
super
This site is really for us student….will like to keep in touch