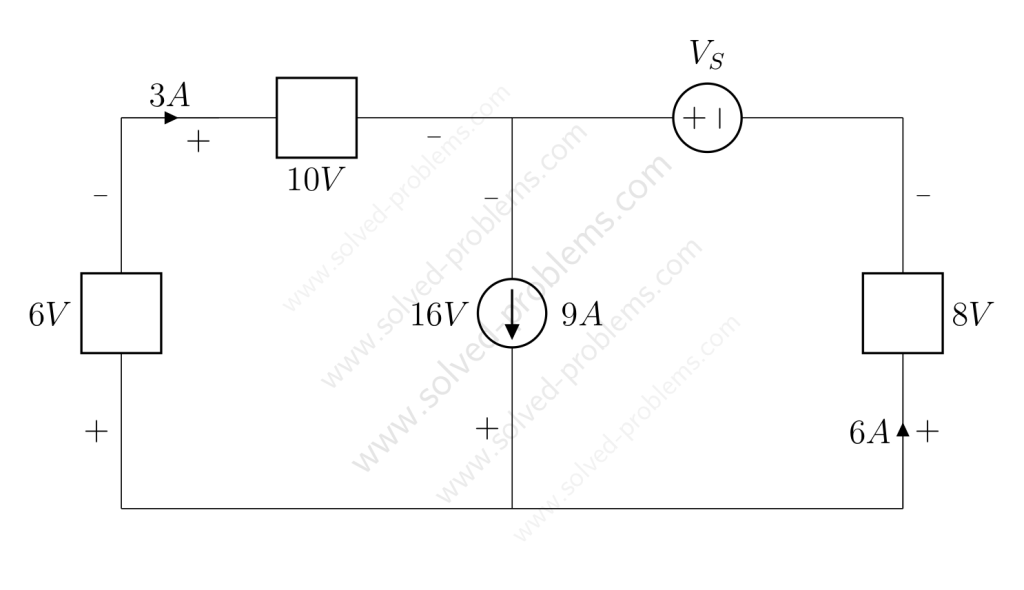
Is the source Vs in the circuit absorbing or supplying power, and how much?
Tag: Independent Sources
-
Electrical Circuit Contest – Win $10!
What’s up? We are going to have fun!
This is our first contest for electrical circuits. Solve the problem, submit your answers and cross your fingers to be the lucky winner!Problem
Find
and 
:
-
Solve Using Current Division Rule
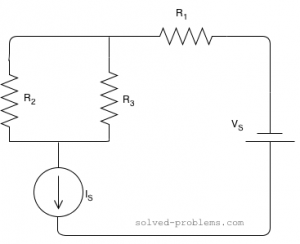
Find current of resistors, use the current division rule.
Suppose that
, 
, 
, 
and 
Solution:
and 
are parallel. The current of 
is passing through them and it is actually divided between them. The branch with lower resistance has higher current because electrons can pass through that easier than the other branch. Using the current division rule, we get
(more…) -
Mesh Analysis – Supermesh
Solve the circuit and find the power of sources:
, 
, , 
, , 
.Solution:
There are three meshes in the circuit. So, we need to assign three mesh currents. It is better to have all the mesh currents loop in the same direction (usually clockwise) to prevent errors when writing out the equations.
(more…) -
Find currents using KVL
Find resistor currents using KVL.
Solution:
and 
are parallel. So the voltage across is equal to . This can be also calculated using KVL in the left hand side loop: -
Thévenin’s Theorem – Circuit with Two Independent Sources
Use Thévenin’s theorem to determine
.
Fig. (1-27-1) – Circuit with two independent sources Solution
Lets break the circuit at the
load as shown in Fig. (1-27-2).
(more…) -
Ideal Independent Sources
1) Ideal Independent Voltage Sources
An ideal independent voltage source is a two-terminal circuit element where the voltage across it
a) is independent of the current through it
b) can be specified independently of any other variable in a circuit.
There are two symbols for ideal independent voltage source in circuit theory:
Symbol for Constant Independent Voltage Source -
Problem 1-15: Power of Independent Sources
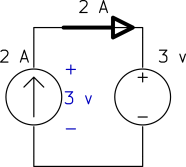
Determine the power of each source.
a)
b)
Solution
a) The current source keeps the current of the loop
and the voltage source keeps the voltage across the current source 
as shown below.
(more…) -
Problem 1-14: Current of A Voltage Source
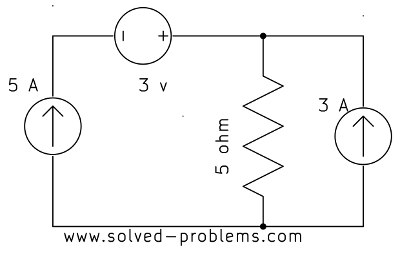
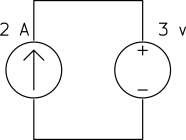
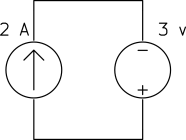
Find the current passing through the voltage source:
a)
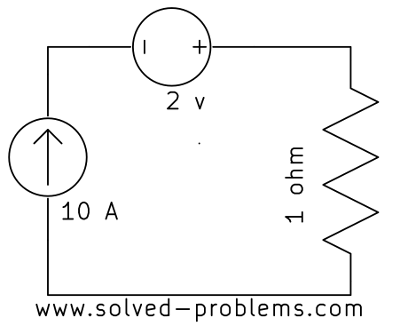
b)
Solution
a) The voltage source is in series with the current source. Since by definition a current source keeps the current passing through itself constant and the voltage source is in series with the current source, it should have the same current
.
(more…) -
Problem 1-13: Voltage of A Current Source
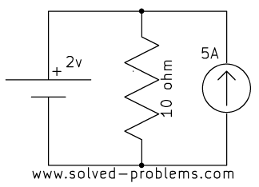
Find voltages across the current sources.
a)
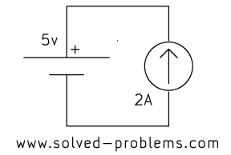
b)
c)
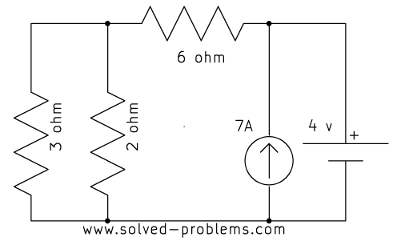
d)
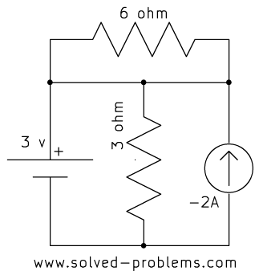
e)
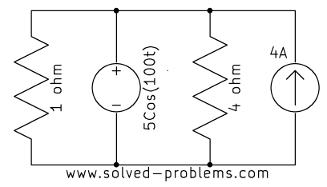
Solution
In each case, the current source is parallel with a voltage source. Therefore, the voltage across the current source is equal to the voltage of the voltage source, regardless of other elements.
(more…)
