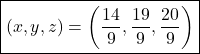Cramer’s Rule is a powerful method for solving systems of linear equations using determinants. It is particularly effective for small systems where calculating determinants manually is feasible. In this post, we will explain the method step-by-step and provide examples to help you master the technique.
What is Cramer’s Rule?
Cramer’s Rule is applicable to systems of linear equations where the number of equations matches the number of variables. The system:
![Rendered by QuickLaTeX.com \[\begin{cases}a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2 \\\vdots \\a_{n1}x_1 + a_{n2}x_2 + \dots + a_{nn}x_n = b_n\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-97d043977401f9612fa18a9affc8b93d_l3.png)
can be expressed in matrix form as:
![]()
where ![]() is the coefficient matrix,
is the coefficient matrix, ![]() is the vector of variables, and
is the vector of variables, and ![]() is the constants vector.
is the constants vector.
To solve for ![]() using Cramer’s Rule:
using Cramer’s Rule:
- Compute the determinant of the coefficient matrix,
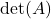 .
. - Replace the
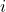 -th column of
-th column of 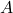 with
with 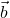 to create a new matrix
to create a new matrix 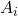 .
. - Solve for each variable using the formula:
![]()
provided ![]() .
.
Steps to Solve Using Cramer’s Rule
- Write the coefficient matrix
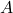 and constants vector
and constants vector 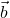 .
. - Compute
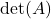 .
. - For each variable
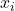 :
:
- Replace the
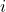 -th column of
-th column of 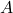 with\ ( \vec{b} \) to form
with\ ( \vec{b} \) to form 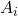 .
. - Compute
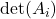 .
. - Solve for
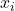 using
using 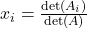 .
.
Example 1: Solving a 2×2 System
Consider the system:
![Rendered by QuickLaTeX.com \[\begin{cases}x + 2y = 5 \\3x - y = 4\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-1d2de21cce6ab26e5b4520db96b0ab29_l3.png)
Step 1: Write the Coefficient Matrix and Constants Vector
![]()
Step 2: Compute ![]()
![]()
![]()
Step 3: Solve for Each Variable
- Replace the 1st column of
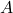 with
with 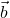 to get
to get 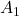 :
:
![]()
Compute ![]() :
:
![]()
![]()
Solve for ![]() :
:
![]()
- Replace the 2nd column of
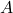 with
with 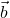 to get
to get 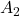 :
:
![]()
Compute ![]() :
:
![]()
![]()
Solve for ![]() :
:
![]()
Solution:
![]()
Below, you can see the lines defined by this system of equations and their intersection point, which represents the solution to the system.

Example 2: Solving a 3×3 System
Solve the system:
![Rendered by QuickLaTeX.com \[\begin{cases}2x + y - z &= 1, \\3x - 2y + 4z &= 7, \\x + 3y - 2z &= -3.\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-63148886e50dccba76909971a1a33e5b_l3.png)
Step 1: Write the coefficient matrix 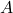 and constants vector
and constants vector 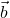 :
:
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}2 & 1 & -1 \\3 & -2 & 4 \\1 & 3 & -2\end{bmatrix}, \quad\vec{b} = \begin{bmatrix}1 \ 7 \ -3\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-c4f7dc8db40136b7dc0830ab78b2476b_l3.png)
Step 2: Compute 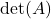 :
:
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) = &2(-2 \times -2 - 4 \times 3) \\&- 1(3 \times -2 - 4 \times 1) \\&- 1(3 \times 3 - (-2 \times 1)).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-7e6f3493236bdaa29628c3a9d7883f6a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) &= 2(4 - 12) - 1(-6 - 4) - 1(9 + 2) \\&= 2(-8) + 10 - 11 \\ &= -16 + 10 - 11 \\&= -17.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-b06feb47bb4a8485aac5559871b62d37_l3.png)
Step 3: Solve for 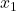 ,
, 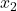 , and
, and 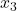 :
:
Solve for 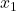 :
:
Replace the first column of ![]() with
with ![]() :
:
![Rendered by QuickLaTeX.com \[A_1 = \begin{bmatrix}1 & 1 & -1 \\7 & -2 & 4 \\-3 & 3 & -2\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-04f773ecc029ab003a869f6477812d5a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_1) = &1(-2 \times -2 - 4 \times 3) \\&- 1(7 \times -2 - 4 \times -3) \\&+ (-1)(7 \times 3 - (-2 \times -3)).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-070b1fd4066483e47650f91f14df61ad_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_1) &= 1(4 - 12) - 1(-14 + 12) - (21 - 6) \\&= -8 + 2 - 15 \\&= -21.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-269adc73905ad44f54b439e556482514_l3.png)
![]()
Solve for 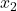 :
:
Replace the second column of ![]() with
with ![]() :
:
![Rendered by QuickLaTeX.com \[A_2 = \begin{bmatrix}2 & 1 & -1 \\3 & 7 & 4 \\1 & -3 & -2\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-b1ffe3eb8d53f0640d9f702ab7e92cf5_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_2) = &2(7 \times -2 - 4 \times -3) \\&- 1(3 \times -2 - 4 \times 1) \\&+ (-1)(3 \times -3 - 7 \times 1).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-39bef044188e00db0b82424eb41f138c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_2) &= 2(-14 +12) - 1(-6 - 4) - 1(-9 - 7) \\&= 2(-2) + 10 +16 \\&= -4 + 10 + 16 \\&= 22.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-6a4c92976f24cbe94601f9fd0bf90a6b_l3.png)
![]()
Solve for 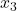 :
:
Replace the third column of ![]() with
with ![]() :
:
![Rendered by QuickLaTeX.com \[A_3 = \begin{bmatrix}2 & 1 & 1 \\3 & -2 & 7 \\1 & 3 & -3\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-b34572107f0ba5ad288936f0a7179b39_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_3) = &2(-2 \times -3 - 7 \times 3) \\&- 1(3 \times -3 - 7 \times 1) \\&+ 1(3 \times 3 - (-2 \times 1)).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-9d8ce91e2f80400e4c71a0621729527a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_3) &= 2(6 - 21) - 1(-9 - 7) + 1(9 + 2) \\&= 2(-15) + 16 + 11 \\&= -30 + 16 + 11 \\&= -3.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-a9b8410a6883b49c96e29b196b9d484c_l3.png)
![]()
Solution:
![]()
Below is an interactive plot displaying three planes defined by the system of equations, along with their intersection point, which represents the solution to the system. You can change the viewpoint by dragging the plot to explore the relationship between the planes and their intersection more effectively. Enjoy visualizing the solution!
Example 3: Special Case – No Solution
Solve the system:
![Rendered by QuickLaTeX.com \[\begin{cases}x + y + z &= 2, \\2x + 2y + 2z &= 5, \\x - y + z &= 1.\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-96ee6b99b6aaeff01c72b687b16ade6f_l3.png)
Step 1: Write the coefficient matrix 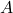 and constants vector
and constants vector 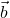 :
:
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}1 & 1 & 1 \\2 & 2 & 2 \\1 & -1 & 1\end{bmatrix}, \quad\vec{b} = \begin{bmatrix}2 \ 5 \ 1\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-8183ba0bea98211386ab5eff2bdd919d_l3.png)
Step 2: Compute 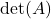 :
:
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) &= 1(2 \times 1 - 2 \times -1) \\&- 1(2 \times 1 - 2 \times 1) \\&+ 1(2 \times -1 - 2 \times 1).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-ef8f5a32175cb45334a79e21a86cce2c_l3.png)
![]()
Since ![]() , the system is inconsistent and has no solution.
, the system is inconsistent and has no solution.
Below, you can see a plot of three planes defined by this system of equations. You can change the viewpoint by dragging the plot for a better perspective. As you observe, these three planes do not intersect at any point, indicating that there is no solution for this system of equations.
Example 4: Special Case – Infinitely Many Solutions
Solve the system:
![Rendered by QuickLaTeX.com \[\begin{cases}x + y + z &= 3, \\2x + 2y + 2z &= 6, \\x - y + z &= 1.\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-89fe91bafef4e6274efc429a63f64d87_l3.png)
Step 1: Write the coefficient matrix 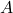 and constants vector
and constants vector 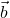 :
:
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}1 & 1 & 1 \\2 & 2 & 2 \\1 & -1 & 1\end{bmatrix}, \quad\vec{b} = \begin{bmatrix}3 \ 6 \ 1\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-d99e9cd2bc42f4893f091c69781a6dfd_l3.png)
Step 2: Compute 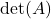 :
:
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) =& 1(2 \times 1 - 2 \times -1) \\&- 1(2 \times 1 - 2 \times 1) \\&+ 1(2 \times -1 - 2 \times 1).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-22ecca84025676a297dacb93c4ccb97b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) &= 1(2 + 2) - 1(2 - 2) + 1(-2 - 2) \\&= 4 - 0 - 4 \\&= 0.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-0e8f881cd5ec6f6da44b65bf383f3d3f_l3.png)
Since ![]() , we check consistency.
, we check consistency.
The second equation is a multiple of the first, indicating a dependency between them. As a result, the system has infinitely many solutions. Essentially, instead of three distinct equations, we only have two, which means there are two planes that intersect along a line, resulting in infinitely many solutions.Below, you can see a plot of three planes defined by this system of equations. You can change the viewpoint by dragging the plot for a better perspective. To observe the relationship between the planes, you can toggle their visibility by clicking on their names in the legend. You’ll notice that the first and second planes overlap completely. The infinitely many solutions for this system of equations can be expressed as the line ![]()
Python Code
Here is the Python code to define and solve the examples above . It includes calculations for determinants and solutions for each case.
import numpy as np
# Function to compute determinant of a matrix
def determinant(matrix):
return round(np.linalg.det(matrix), 2)
# Function to solve a system using Cramer's Rule
def cramers_rule(A, b):
det_A = determinant(A)
if det_A == 0:
print("Det(A) = 0, system may have no solution or infinitely many solutions.")
return None
solutions = []
n = len(b)
for i in range(n):
Ai = np.copy(A)
Ai[:, i] = b
det_Ai = determinant(Ai)
solutions.append(det_Ai / det_A)
return solutions
# Example 1: Solving a 2x2 System
A1 = np.array([[1, 2],
[3, -1]])
b1 = np.array([5, 4])
print("Example 1: Solving a 2x2 System")
solutions_1 = cramers_rule(A1, b1)
if solutions_1:
print(f"Solutions: x1 = {solutions_1[0]}, x2 = {solutions_1[1]}")
# Example 2: Solving a 3x3 System
A2 = np.array([[2, 1, -1],
[3, -2, 4],
[1, 3, -2]])
b2 = np.array([1, 7, -3])
print("\nExample 2: Solving a 3x3 System")
solutions_2 = cramers_rule(A2, b2)
if solutions_2:
print(f"Solutions: x1 = {solutions_2[0]}, x2 = {solutions_2[1]}, x3 = {solutions_2[2]}")
# Example 3: No Solution
A3 = np.array([[1, 1, 1],
[2, 2, 2],
[1, -1, 1]])
b3 = np.array([2, 5, 1])
print("\nExample 3: No Solution")
det_A3 = determinant(A3)
if det_A3 == 0:
print("Det(A) = 0. The system has no solution (inconsistent).")
# Example 4: Infinitely Many Solutions
A4 = np.array([[1, 1, 1],
[2, 2, 2],
[1, -1, 1]])
b4 = np.array([3, 6, 1])
print("\nExample 4: Infinitely Many Solutions")
det_A4 = determinant(A4)
if det_A4 == 0:
print("Det(A) = 0. The system has infinitely many solutions (dependent equations).")

![Rendered by QuickLaTeX.com \[\begin{cases}x + 2y + z &= 8 \\2x + y - z &= 3 \\3x - y + 2z &= 7\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-670cf71cf0b8a9a9ed4d488ebd449ac2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}&\frac{14}{9} + 2\left(\frac{19}{9} \right) + \frac{20}{9} \\&= \frac{14}{9} + \frac{38}{9} + \frac{20}{9} \\&= \frac{14+38+20}{9} \\&= 8 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-f65b8937d5e92add30b938d93ee1678f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}&2(\frac{14}{9}) + \frac{19}{9} - \frac{20}{9} \\&= \frac{28}{9} + \frac{19}{9} - \frac{20}{9} \\&= - \frac{28+19-20}{9} \\&= 3 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-384c4cff6d31635011aba128086f43bc_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}&3(\frac{14}{9}) - \frac{19}{9} + 2\left(\frac{20}{9} \right) \\&= \frac{42}{9} - \frac{19}{9} + \frac{40}{9} \\&= \frac{42-19+40}{3} \\&= 7 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-6d693017f60eef2ad778aa9649d58866_l3.png)