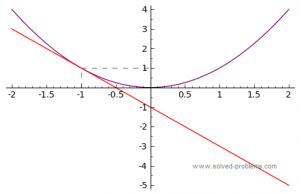
Differentiate ![]() by using the chain rule.
by using the chain rule.
Category: Derivative
Solved Problems in Derivatives
-
Problem 2-11: Differentiating by Chain Rule
-
Problem 2-9: Differentiating Polynomial and Rational Functions
Differentiate
a)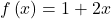
b)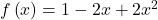
c)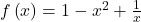
d)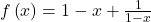
Solution
The following rules can be used:
I)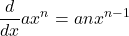
II)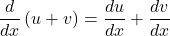
III)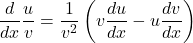
(more…)