Differentiate
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Solution
The following rules can be used:
I) ![]()
II) ![]()
III) ![]()
a) ![]()
![]()

b) ![]()
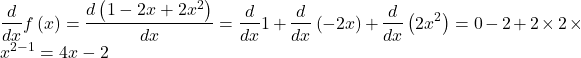

c) ![]()
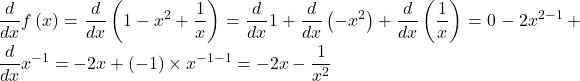

d) ![]()
![]()
Let’s use rule III to find ![]() .
.
![]()
![]()
Therefore,
![]()

Differentiate
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Solution
The following rules can be used:
I) ![]()
II) ![]()
III) ![]()
a) ![]()
![]()

b) ![]()
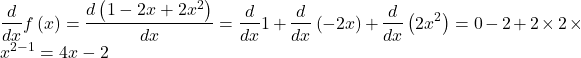

c) ![]()
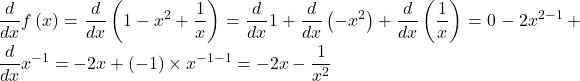

d) ![]()
![]()
Let’s use rule III to find ![]() .
.
![]()
![]()
Therefore,
![]()

It’s wery useful site for us.
It’s very useful wapsite for us.
Fine way of telling, and good article to get data on the topic of my presentation focus, which i am going to convey in university.
Leave a Reply