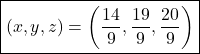When solving systems of linear equations, the elimination method is one of the most popular and systematic approaches. This method involves adding or subtracting equations to eliminate one of the variables, allowing us to solve for the other. Once one variable is found, we substitute it back into one of the original equations to find the second variable.
Steps for Solving Using the Elimination Method
Here are the general steps for solving a system of equations using the elimination method:
- Align the equations so that like terms (variables and constants) are in columns.
- Eliminate one variable by adding or subtracting the equations. If necessary, multiply one or both equations by a constant to align coefficients.
- Solve for the remaining variable.
- Substitute the solution back into one of the original equations to find the other variable.
- Verify the solution by substituting the values into both original equations.
Example 1: A Simple Elimination Scenario
Solve the following system of equations:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2x + 3y &= 8 \\ 4x - 3y &= 10 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-bc8ec49f0ccf7edf0594d82caa5c3273_l3.png)
Step 1: Align the equations
The equations are already aligned:
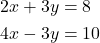
Step 2: Eliminate one variable
Notice that the coefficients of 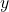 are opposites:
are opposites: 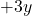 in the first equation and
in the first equation and 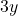 in the second equation. To eliminate
in the second equation. To eliminate 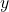 , add the two equations:
, add the two equations:
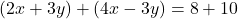
Simplify:
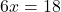
Step 3: Solve for 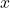
Divide both sides by 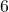 :
:
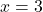
Step 4: Solve for 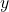
Substitute 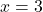 into one of the original equations. Let’s use the first equation:
into one of the original equations. Let’s use the first equation:
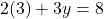
Simplify:

Subtract 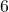 from both sides:
from both sides:
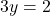
Divide by 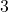 :
:
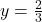
Step 5: Verify the solution
Substitute 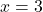 and
and 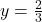 into both original equations to confirm they work:
into both original equations to confirm they work:
- For
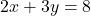 :
: 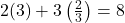
- For
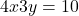 :
: 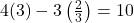
Thus, the solution is: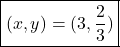
Visualization
In the plot below, you can see the two lines represented by the equations. The point of intersection, marked on the graph, represents the solution to the system of equations.
Example 2: Multiplying to Align Coefficients
Solve the following system of equations:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2y + 3x&= 12 \\ 5x - 4y &= -2 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-ff1b3e2343496d59c99b4d62f2d01730_l3.png)
Step 1: Align the equations
The equations are aligned below:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 3x + 2y &= 12 \\ 5x - 4y &= -2 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-9c46fb85cf62255db4188239af25859b_l3.png)
Step 2: Eliminate one variable
We need to align the coefficients of either 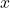 or
or 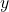 . Let’s eliminate
. Let’s eliminate 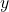 . To do this, multiply the first equation by
. To do this, multiply the first equation by 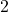 and the second equation by
and the second equation by 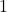 (so that the coefficients of
(so that the coefficients of 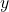 are opposites):
are opposites):
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2(3x + 2y) &= 2(12) \\ 1(5x - 4y) &= 1(-2) \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-d083c16ef09acab55669c713eefd0d66_l3.png)
This gives us:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 6x + 4y &= 24 \\ 5x - 4y &= -2 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-45993ca5d00c53028794435998a133b5_l3.png)
Now, add the equations to eliminate 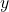 :
:
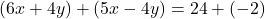
Simplify: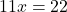
Step 3: Solve for 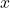
Divide both sides by  :
: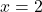
Step 4: Solve for 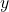
Substitute 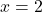 into one of the original equations. Let’s use the first equation:
into one of the original equations. Let’s use the first equation:
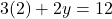
Simplify:
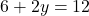
Subtract 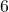 from both sides:
from both sides:
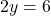
Divide by 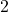 :
:
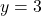
Step 5: Verify the solution
Substitute 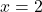 and
and 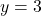 into both original equations to confirm they work:
into both original equations to confirm they work:
- For
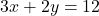 :
: 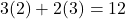
- For
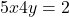 :
: 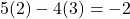
Thus, the solution is: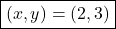
Visualization
The plot below illustrates the two lines corresponding to the equations. The intersection point indicates the solution to the system of equations.
Example 3: Infinite Solutions
Sometimes, a system of equations can have infinite solutions (the equations represent the same line). Let’s look at an example.
Solve the following system:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2x + 4y &= 8 \\ x + 2y &= 4 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-59b67ad66fa8e657f7dccfce4f0e1539_l3.png)
Step 1: Align the equations
The equations are already aligned:
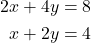
Step 2: Eliminate one variable
Notice that the second equation is just half of the first. Multiply the second equation by 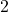 :
:
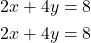
Subtract the second equation from the first:
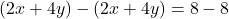
Simplify:
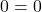
This is a true statement, meaning the two equations represent the same line. Therefore, there are infinite solutions.
Visualization
The plot below shows the two equations as overlapping lines, indicating that every point on the line is a solution to the system.
Example 4: No Solution
Also, a system of equations can have no solution (the lines are parallel). Here is an example.
Solve the following system of equations:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2x + 3y &= 6 \\ 6y + 4x &= 15 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-4e3306e629ff4a45323d7da8285471b1_l3.png)
Step 1: Align the equations
The equations are aligned below:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2x + 3y &= 6 \ 4x + 6y &= 15 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-dcf7c2db959eec1957996d6e8b58caf5_l3.png)
Step 2: Eliminate one variable
To eliminate one variable, we need to make the coefficients of either 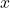 or
or 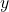 the same. Let’s eliminate
the same. Let’s eliminate 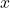 . Multiply the first equation by
. Multiply the first equation by 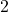 so that the coefficients of
so that the coefficients of 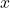 : match:
: match:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 2(2x + 3y) &= 2(6) \\ 4x + 6y &= 15 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-86dac4293ceb9fdb9a6f15d528fee907_l3.png)
This gives us:
![Rendered by QuickLaTeX.com \begin{aligned}[t] 4x + 6y &= 12 \\ 4x + 6y &= 15 \end{aligned}](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-129fdac23ce5b6dbfff2d6107cdd2979_l3.png)
Now subtract the first equation from the second:
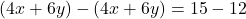
Simplify:
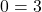
This is a false statement, meaning the system of equations has no solution. The two lines are parallel and never intersect.
Visualization
The plot below illustrates the two parallel lines, confirming that there is no point of intersection. This graphical representation helps to visualize why the system has no solution.
Example 5: Solving a 3×3 System of Equations
Solve the following system of equations:
![Rendered by QuickLaTeX.com \[\begin{cases}x + 2y + z &= 8 \\2x + y - z &= 3 \\3x - y + 2z &= 7\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-670cf71cf0b8a9a9ed4d488ebd449ac2_l3.png)
Step 1: Align the equations
The equations are already aligned:
![Rendered by QuickLaTeX.com \[\begin{cases}x + 2y + z &= 8 \\2x + y - z &= 3 \\3x - y + 2z &= 7\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-670cf71cf0b8a9a9ed4d488ebd449ac2_l3.png)
Step 2: Eliminate one variable
We will eliminate ( z ) first. To do this, we can use the first two equations. We can add the first equation to the second equation after adjusting the coefficients of ( z ).
First, we can rewrite the second equation to align ( z ):
![Rendered by QuickLaTeX.com \[2x + y - z = 3 \quad \text{(no change needed)}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-f4ada64d7383572e2fa9f7bace50d7dd_l3.png)
Now, we can add the first equation to the second equation:
![Rendered by QuickLaTeX.com \[\begin{aligned}(x + 2y + z) + (2x + y - z) &= 8 + 3 \\3x + 3y &= 11\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-32ccc9bb94f7bfc8b42b92ea935e326d_l3.png)
Simplify:
(Eq 4) ![Rendered by QuickLaTeX.com \[x + y = \frac{11}{3} \quad \]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-07485d56420abfe738067959247add55_l3.png)
Next, we will eliminate ( z ) using the first and third equations. We can rewrite the first equation to align ( z ):
![Rendered by QuickLaTeX.com \[2x + 4y + 2z = 16 \quad \text{(multiplied by two)}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-ae7fc80b22eb15f2223866498a0b4905_l3.png)
Now, we can add the first equation to the third equation after adjusting the coefficients of ( z ):
![Rendered by QuickLaTeX.com \[(3x - y + 2z) - (2x + 4y + 2z) &= 7 - 16\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-c544c12e8c736a019a2808159f39a517_l3.png)
Simplify:
(Eq 5) ![Rendered by QuickLaTeX.com \[x - 5y = -9 \quad \]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-32526e46830b33ff59e1636a964ac2db_l3.png)
Step 3: Solve for one variable
Now we have two new equations (Equation 4 and Equation 5):
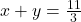 (Equation 4)
(Equation 4)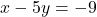 (Equation 5)
(Equation 5)
We can solve Equation 4 for 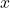 :
:
![Rendered by QuickLaTeX.com \[x = \frac{11}{3} - y\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-7c0b983e4009bb5cde4b821160389fb0_l3.png)
Substituting 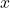 into Equation 5:
into Equation 5:
![Rendered by QuickLaTeX.com \[\left(\frac{11}{3} - y\right) - 5y = -9\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-6468bdfbe7e660dbbd78a4bf7a9ec597_l3.png)
Simplify:
![Rendered by QuickLaTeX.com \[\frac{11}{3} - y - 5y = -9\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-704b2ac8807647c034f120b9c7b14067_l3.png)
Combine like terms:
![Rendered by QuickLaTeX.com \[\frac{11}{3} - 6y = -9\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-8b925930a2d3c68f6fabf8bac68644d9_l3.png)
Multiply through by 3 to eliminate the fraction:
![Rendered by QuickLaTeX.com \[11 - 18y = -27\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-a06d2635b6425aeb289a8d16d4fe1114_l3.png)
Subtract 11 from both sides:
![Rendered by QuickLaTeX.com \[-18y = -38\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-1d8a708e90d8e134c2f994dfe5c887bc_l3.png)
Divide by -18:
![Rendered by QuickLaTeX.com \[y = \frac{19}{9}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-4215264acf4570cb4380ecc940eca2d7_l3.png)
Step 4: Solve for 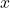 and
and 
Substituting 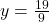 back into Equation 4:
back into Equation 4:
![Rendered by QuickLaTeX.com \[x + \frac{19}{9} = \frac{11}{3}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-30c33398b783dd3cb4019a995f425427_l3.png)
Subtract 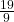 from both sides:
from both sides:
![Rendered by QuickLaTeX.com \[x = \frac{11}{3} - \frac{19}{9} = \frac{33-19}{9} = \frac{14}{9}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-2fdc7e7839cea24efce5f81b058b6cb5_l3.png)
Now, substitute 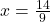 and
and 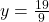 back into the first original equation to find
back into the first original equation to find  :
:
![Rendered by QuickLaTeX.com \[ \frac{14}{9} + 2\left( \frac{19}{9}\right) + z = 8\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-75bbbd546c68327df4919bbd86a70680_l3.png)
Simplify:
![Rendered by QuickLaTeX.com \[ \frac{14}{9} + \frac{38}{9} + z = 8\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-912a5615f48d442bfbf33c19b026bd79_l3.png)
Combine the fractions:
![Rendered by QuickLaTeX.com \[\frac{52}{9} + z = 8\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-67ffc3656739a1925b33e36a10a5e7cc_l3.png)
Subtract 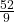 from both sides:
from both sides:
![Rendered by QuickLaTeX.com \[z = 8 - \frac{52}{9} = \frac{72}{9} - \frac{52}{9} = \frac{20}{9}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-f2cbce1d38d5aa8ee084785382abbd44_l3.png)
Step 5: Verify the solution
Substitute 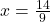 ,
, 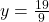 , and
, and 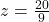 into all original equations to confirm they work:
into all original equations to confirm they work:
- For
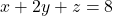 :
:
![Rendered by QuickLaTeX.com \[\begin{aligned}&\frac{14}{9} + 2\left(\frac{19}{9} \right) + \frac{20}{9} \\&= \frac{14}{9} + \frac{38}{9} + \frac{20}{9} \\&= \frac{14+38+20}{9} \\&= 8 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-f65b8937d5e92add30b938d93ee1678f_l3.png)
- For
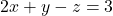 :
:
![Rendered by QuickLaTeX.com \[\begin{aligned}&2(\frac{14}{9}) + \frac{19}{9} - \frac{20}{9} \\&= \frac{28}{9} + \frac{19}{9} - \frac{20}{9} \\&= - \frac{28+19-20}{9} \\&= 3 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-384c4cff6d31635011aba128086f43bc_l3.png)
- For
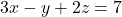 :
:
![Rendered by QuickLaTeX.com \[\begin{aligned}&3(\frac{14}{9}) - \frac{19}{9} + 2\left(\frac{20}{9} \right) \\&= \frac{42}{9} - \frac{19}{9} + \frac{40}{9} \\&= \frac{42-19+40}{3} \\&= 7 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-6d693017f60eef2ad778aa9649d58866_l3.png)
Thus, the solution is: 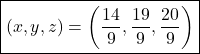
Visualization
The plot below illustrates the three planes represented by the equations. The point of intersection, marked on the graph, represents the unique solution to the system of equations.
Key Takeaways
- The elimination method is a powerful way to solve systems of equations by eliminating one variable at a time.
- Always align your equations properly and, if necessary, multiply through by constants to align coefficients.
- Verify your solution by substituting the values into both original equations.
- Keep an eye out for special cases like infinite solutions or no solution.
![]() .
.
![]()




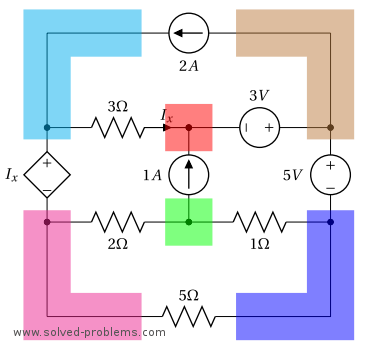
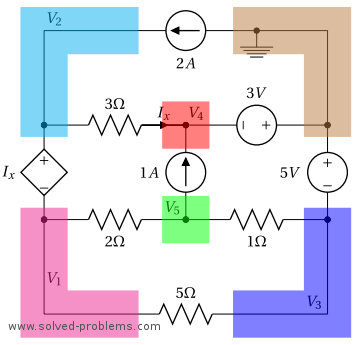







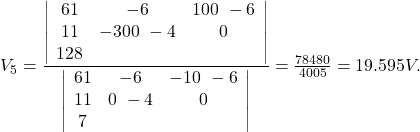
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} 61 V_3-6 V_4-10 V_5=100 \\ -6V_3+11 V_4=-300 \\ -4 V_3+7V_5=128 \end{array} \right.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-265860250d9eab754e916d35e60577c6_l3.png)

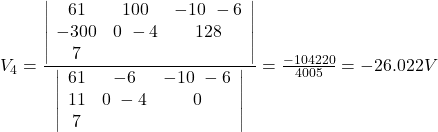






![Rendered by QuickLaTeX.com \[\begin{cases}a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2 \\\vdots \\a_{n1}x_1 + a_{n2}x_2 + \dots + a_{nn}x_n = b_n\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-97d043977401f9612fa18a9affc8b93d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}x + 2y = 5 \\3x - y = 4\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-1d2de21cce6ab26e5b4520db96b0ab29_l3.png)

![Rendered by QuickLaTeX.com \[\begin{cases}2x + y - z &= 1, \\3x - 2y + 4z &= 7, \\x + 3y - 2z &= -3.\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-63148886e50dccba76909971a1a33e5b_l3.png)
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}2 & 1 & -1 \\3 & -2 & 4 \\1 & 3 & -2\end{bmatrix}, \quad\vec{b} = \begin{bmatrix}1 \ 7 \ -3\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-c4f7dc8db40136b7dc0830ab78b2476b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) = &2(-2 \times -2 - 4 \times 3) \\&- 1(3 \times -2 - 4 \times 1) \\&- 1(3 \times 3 - (-2 \times 1)).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-7e6f3493236bdaa29628c3a9d7883f6a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) &= 2(4 - 12) - 1(-6 - 4) - 1(9 + 2) \\&= 2(-8) + 10 - 11 \\ &= -16 + 10 - 11 \\&= -17.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-b06feb47bb4a8485aac5559871b62d37_l3.png)
![Rendered by QuickLaTeX.com \[A_1 = \begin{bmatrix}1 & 1 & -1 \\7 & -2 & 4 \\-3 & 3 & -2\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-04f773ecc029ab003a869f6477812d5a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_1) = &1(-2 \times -2 - 4 \times 3) \\&- 1(7 \times -2 - 4 \times -3) \\&+ (-1)(7 \times 3 - (-2 \times -3)).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-070b1fd4066483e47650f91f14df61ad_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_1) &= 1(4 - 12) - 1(-14 + 12) - (21 - 6) \\&= -8 + 2 - 15 \\&= -21.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-269adc73905ad44f54b439e556482514_l3.png)
![Rendered by QuickLaTeX.com \[A_2 = \begin{bmatrix}2 & 1 & -1 \\3 & 7 & 4 \\1 & -3 & -2\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-b1ffe3eb8d53f0640d9f702ab7e92cf5_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_2) = &2(7 \times -2 - 4 \times -3) \\&- 1(3 \times -2 - 4 \times 1) \\&+ (-1)(3 \times -3 - 7 \times 1).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-39bef044188e00db0b82424eb41f138c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_2) &= 2(-14 +12) - 1(-6 - 4) - 1(-9 - 7) \\&= 2(-2) + 10 +16 \\&= -4 + 10 + 16 \\&= 22.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-6a4c92976f24cbe94601f9fd0bf90a6b_l3.png)
![Rendered by QuickLaTeX.com \[A_3 = \begin{bmatrix}2 & 1 & 1 \\3 & -2 & 7 \\1 & 3 & -3\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-b34572107f0ba5ad288936f0a7179b39_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_3) = &2(-2 \times -3 - 7 \times 3) \\&- 1(3 \times -3 - 7 \times 1) \\&+ 1(3 \times 3 - (-2 \times 1)).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-9d8ce91e2f80400e4c71a0621729527a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A_3) &= 2(6 - 21) - 1(-9 - 7) + 1(9 + 2) \\&= 2(-15) + 16 + 11 \\&= -30 + 16 + 11 \\&= -3.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-a9b8410a6883b49c96e29b196b9d484c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}x + y + z &= 2, \\2x + 2y + 2z &= 5, \\x - y + z &= 1.\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-96ee6b99b6aaeff01c72b687b16ade6f_l3.png)
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}1 & 1 & 1 \\2 & 2 & 2 \\1 & -1 & 1\end{bmatrix}, \quad\vec{b} = \begin{bmatrix}2 \ 5 \ 1\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-8183ba0bea98211386ab5eff2bdd919d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) &= 1(2 \times 1 - 2 \times -1) \\&- 1(2 \times 1 - 2 \times 1) \\&+ 1(2 \times -1 - 2 \times 1).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-ef8f5a32175cb45334a79e21a86cce2c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}x + y + z &= 3, \\2x + 2y + 2z &= 6, \\x - y + z &= 1.\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-89fe91bafef4e6274efc429a63f64d87_l3.png)
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix}1 & 1 & 1 \\2 & 2 & 2 \\1 & -1 & 1\end{bmatrix}, \quad\vec{b} = \begin{bmatrix}3 \ 6 \ 1\end{bmatrix}.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-d99e9cd2bc42f4893f091c69781a6dfd_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) =& 1(2 \times 1 - 2 \times -1) \\&- 1(2 \times 1 - 2 \times 1) \\&+ 1(2 \times -1 - 2 \times 1).\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-22ecca84025676a297dacb93c4ccb97b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{split}\det(A) &= 1(2 + 2) - 1(2 - 2) + 1(-2 - 2) \\&= 4 - 0 - 4 \\&= 0.\end{split}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-0e8f881cd5ec6f6da44b65bf383f3d3f_l3.png)




![Rendered by QuickLaTeX.com \[\begin{cases}x + 2y + z &= 8 \\2x + y - z &= 3 \\3x - y + 2z &= 7\end{cases}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-670cf71cf0b8a9a9ed4d488ebd449ac2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}&\frac{14}{9} + 2\left(\frac{19}{9} \right) + \frac{20}{9} \\&= \frac{14}{9} + \frac{38}{9} + \frac{20}{9} \\&= \frac{14+38+20}{9} \\&= 8 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-f65b8937d5e92add30b938d93ee1678f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}&2(\frac{14}{9}) + \frac{19}{9} - \frac{20}{9} \\&= \frac{28}{9} + \frac{19}{9} - \frac{20}{9} \\&= - \frac{28+19-20}{9} \\&= 3 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-384c4cff6d31635011aba128086f43bc_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned}&3(\frac{14}{9}) - \frac{19}{9} + 2\left(\frac{20}{9} \right) \\&= \frac{42}{9} - \frac{19}{9} + \frac{40}{9} \\&= \frac{42-19+40}{3} \\&= 7 \quad \text{\checkmark}\end{aligned}\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-6d693017f60eef2ad778aa9649d58866_l3.png)