Use nodal analysis to solve the circuit shown below and determine the power of node ![]() .
.

I. Identify all nodes in the circuit.
The circuit has five nodes as shown below.

- Top Node (
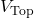 )}: Connected to
)}: Connected to 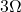 ,
, 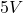 voltage source (
voltage source (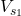 ), and
), and 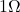 .
. - Middle-Left Node (
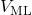 )}: Connected to
)}: Connected to 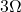 ,
, 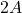 current source (
current source (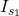 ), and
), and 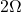 .
. - Middle-Center Node (
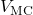 )}: Chosen as the reference node (ground) because it connects the largest number of elements.
)}: Chosen as the reference node (ground) because it connects the largest number of elements. - Middle-Right Node (
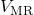 )}: Connected to
)}: Connected to 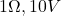 voltage source (
voltage source (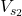 ), and
), and 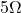 .
. - Bottom Node (
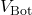 )}: Connected to
)}: Connected to 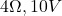 voltage source (
voltage source (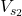 ), and
), and 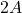 current source (
current source (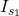 ).
).
II. Select a reference node.
The middle-center node ![]() is chosen as the reference node, with
is chosen as the reference node, with ![]() .
.
III. Assign variables for unknown node voltages.
The unknown node voltages are: ![]() and
and ![]() .
.
The voltage of the Top Node is known because it is connected to the Middle-Right Node (which is the reference node with ![]() ) through a voltage source,
) through a voltage source, ![]() .
.
Since the negative terminal of the voltage source ![]() is connected to the Top Node, the voltage at the Top Node is determined by the polarity of the voltage source.
is connected to the Top Node, the voltage at the Top Node is determined by the polarity of the voltage source.
Thus,
![]()
This result follows directly from the convention that the voltage at the negative terminal of a voltage source is less than the voltage at its positive terminal by the source’s voltage value.
A similar reasoning applies to the Bottom Node. This node is connected to the reference node (Middle-Center Node, ( V = 0 )) through the voltage source ![]() .
.
Since the negative terminal of the voltage source ![]() is connected to the Bottom Node, the voltage at the Bottom Node is determined by the polarity of the voltage source.
is connected to the Bottom Node, the voltage at the Bottom Node is determined by the polarity of the voltage source.
Thus, the voltage at the Bottom Node is:
![]()
As with the Top Node, the voltage at the Bottom Node is calculated directly using the convention that the voltage at the negative terminal of a voltage source is less than the voltage at its positive terminal by the source’s voltage value.
IV. Incorporate dependent sources.
No dependent sources exist, so this step is skipped.
V. Apply Kirchhoff’s Current Law (KCL).
Using ![]() , write the KCL equations for each node.
, write the KCL equations for each node.
Node ![]() :
:
Currents leaving ![]() :
:
![]()
Substitute ![]() :
:
![]()
Simplify:
![]()
![]()
![]()
Node ![]() :
:
Currents leaving ![]() :
:
![]()
Substituting ![]() and
and ![]() :
:
![]()
Multiply through by 20 to clear the fraction:
![]()
![]()
![]()
VI. Handle super-nodes.
There is no super-node in this circuit.
VII: Solve the System of Equations
At this stage, all node voltages are known, and there is no need to solve any additional equations.
Each node voltage has been determined using straightforward reasoning based on the circuit’s components, connections, and the chosen reference node.
Thus, the circuit is fully solved, and we can proceed to calculate any desired quantities, such as currents through resistors or power supplied/absorbed by the sources, using the known node voltages.
VIII. Determine Additional Variables.
Calculating the Power Supplied by ![]()
To calculate the power supplied by the voltage source ![]() , we first need to determine the current flowing through
, we first need to determine the current flowing through ![]() . The current
. The current ![]() consists of two components:
consists of two components:
1. The current flowing through ![]() (the resistor between the Middle-Right Node and the Top Node).
(the resistor between the Middle-Right Node and the Top Node).
2. The current through ![]() (the resistor connected to the Top Node and the Middle-Left Node).
(the resistor connected to the Top Node and the Middle-Left Node).

The current through ![]() , denoted
, denoted ![]() , is calculated using Ohm’s law:
, is calculated using Ohm’s law:
![]()
![]()
The current through ![]() , denoted
, denoted ![]() , is similarly calculated using Ohm’s law:
, is similarly calculated using Ohm’s law:
![]()
![]()
Since ![]() supplies both of these currents, the total current
supplies both of these currents, the total current ![]() is:
is:
![]()
![]()
The power supplied by ![]() is given by:
is given by:
![]()
![]()
The positive power indicates that the voltage source is supplying power to the circuit, consistent with the Positive Sign Convention.
Download the Circuit File
To download the LTspice circuit file for your own simulations, click the link below.Please remember to unzip the file after downloading to access the .asc file for your simulations:

Leave a Reply