Nodal Analysis – Dependent Current Source

Written by

Electrical Circuits, Electrical Circuits Problems, Resistive Circuits

Deploy nodal analysis method to solve the circuit and find the power of the dependent source.

I. Identify all nodes in the circuit.
The circuit has 4 nodes.

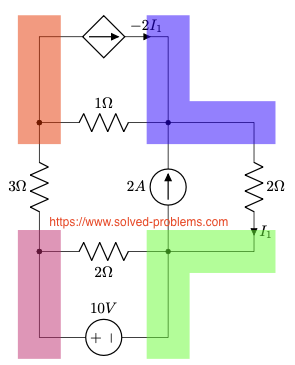
II. Select a reference node. Label this node with the reference (ground) symbol.

All nodes have the same number of elements. We prefer to select one of the nodes connected to the voltage source to avoid having to use a super-node.

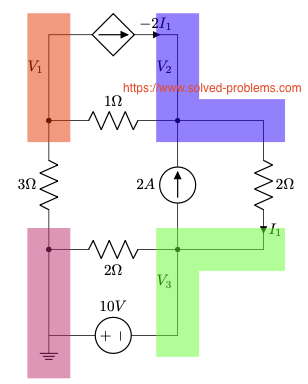
III. Assign variables for unknown node voltages.

We label the remaining three nodes as shown above.

IV. Incorporate dependent sources.

If there are dependent sources in the circuit, write down equations that express their values in terms of node voltages.

There is one dependent source, which is a current controlled current source. We need to write $-2I_1$ in terms of node voltages. $I_1$ is the current passing through the $2\Omega$ – resistor. Applying the Ohm’s law,

$I_1 = \frac{V_2-V_3}{2\Omega}$

.
Hence,

$-2I_1 = V_3-V_2$

V. Apply Kirchhoff’s Current Law (KCL).

Node $V_1$ :

$\frac{V_1}{3 \Omega}+\frac{V_1-V_2}{1\Omega}-2I_1=0$

(1) $to 4V_1-6V_2+3V_3=0$

Node $V_2$ :

$2I_1+\frac{V_2-V_1}{1\Omega}-2A+\frac{V_2-V_3}{2\Omega}=0$

Please note that we avoid using all unknowns except node voltages. Using $I_1$ in this KCL equation introduces an unnecessary unknown to the equations set. Substituting $2I_1 = V_2-V_3$ and rearranging results in:

(2) $-2V_1+5V_2-3V_3=4$

Node $V_3$ has a voltage source connected to. Therefore, $V_3=10V$ .

Substituting this in Eq. 1 and Eq.2 leads to

$\left{\begin{array}{l} 4V_1-6V_2=-30 \ -2V_1+5V_2=34 \end{array}\right.$

VI. Handle super-nodes.
There is no super-node in this circuit.

VII. Solve the System of Equations.
By solving the system of equations,
$V_1=6.75V$ and $V_2=9.5$ .

VIII. Determine Additional Variables.

Now, we need to find the voltage across the dependent current source and the current passing through it. Lets start with $I_1$ .
$I_1 = \frac{V_2-V_3}{2\Omega}=-0.25 A$ .
Assuming positive terminal placed on the node of $V_1$ , the voltage across the dependent current source is $V_1-V_2=-2.75V$ . The current flowing through the dependent current source is $-2I_1=0.5A$ . Therefore the power of the dependent current source is $-2.75 \times 0.5 = -1.375W$ . Because the current direction and the voltage polarity is in accordance with the passive sign convention and the power is negative, the dependent current source is supplying power.

Download the Circuit File

To download the LTspice circuit file for your own simulations, click the link below.Please remember to unzip the file after downloading to access the .asc file for your simulations:

Nodal Analysis – Dependent Current Source.asc Download

dependent current source Nodal Analysis Nodal_Analysis Power

Comments

7 responses to “Nodal Analysis – Dependent Current Source”

February 19, 2012

khans sahil

Thank you sir

Reply
May 29, 2012

Ram Kaushik

thanks a lot !! im passing my test coz of u …. cheers mate 🙂 🙂

Reply
February 25, 2014

Juan dela Cruz

Thanks, but correct me if i’m wrong but all nodes doesn’t have the same number of elements:

*Node 4 has 3 elements = 2 ohms, 3 ohms and 10V

*Node 2 has 4 elements = -2I1 dependet source, 2A current source, 1 ohms and 2 ohms.

*Node 3 has 4 elements = 2 ohms, 10V, 2A current source and 2 ohms.

*Node 1 has 3 elements = 1 ohms, 3 ohms and -2I1 dependet source.

Why choose node 4 with 3 elements as reference node if node 2 and node 3 have 4 elements or the most number of elements?

Reply
July 31, 2014

Chetan Jadhav

Thanks a Lot! It really helped me, made my concepts clear and solved many doubts. Thank you.

Reply
February 28, 2015

makoi beny

it’s more than a lecture’s hall. thanks for this a mazing website

Reply
May 27, 2018

Aakash Yadav

The Best Teacher

Reply
September 6, 2021

ermi

thank you it is wonderful

Reply