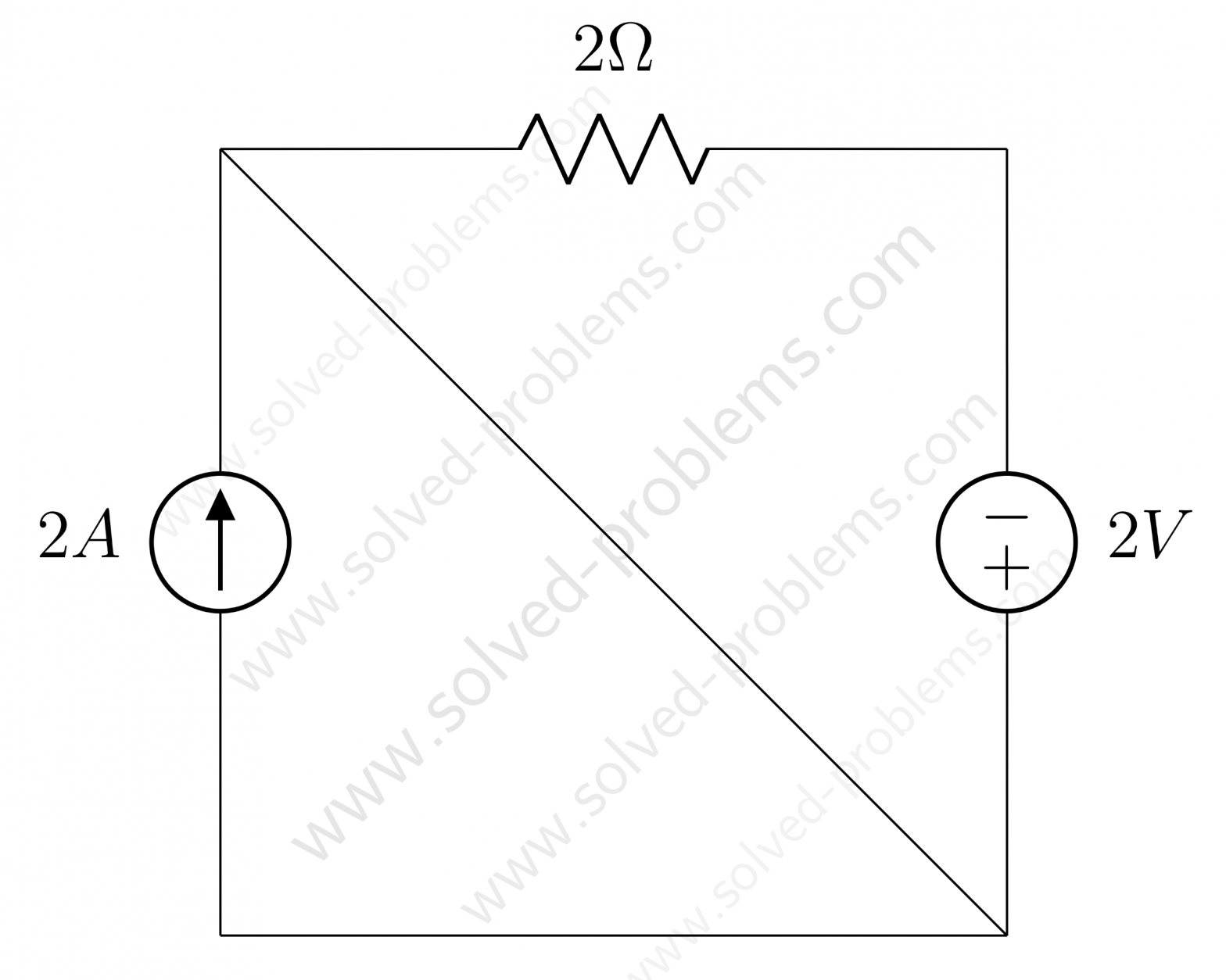
A simple circuit is solved and power absorbed or supplied by each element is determined. KCL as well as Ohm’s law are used in solving the circuit. positive sign convention is used in determining element powers. It is shown and discussed how a source, here current source, can be neither absorbing or supplying power. It is also mentioned that resistors are passive elements and always absorb power/energy.
Category Archives: Electrical Circuits
Power and Energy Conservation
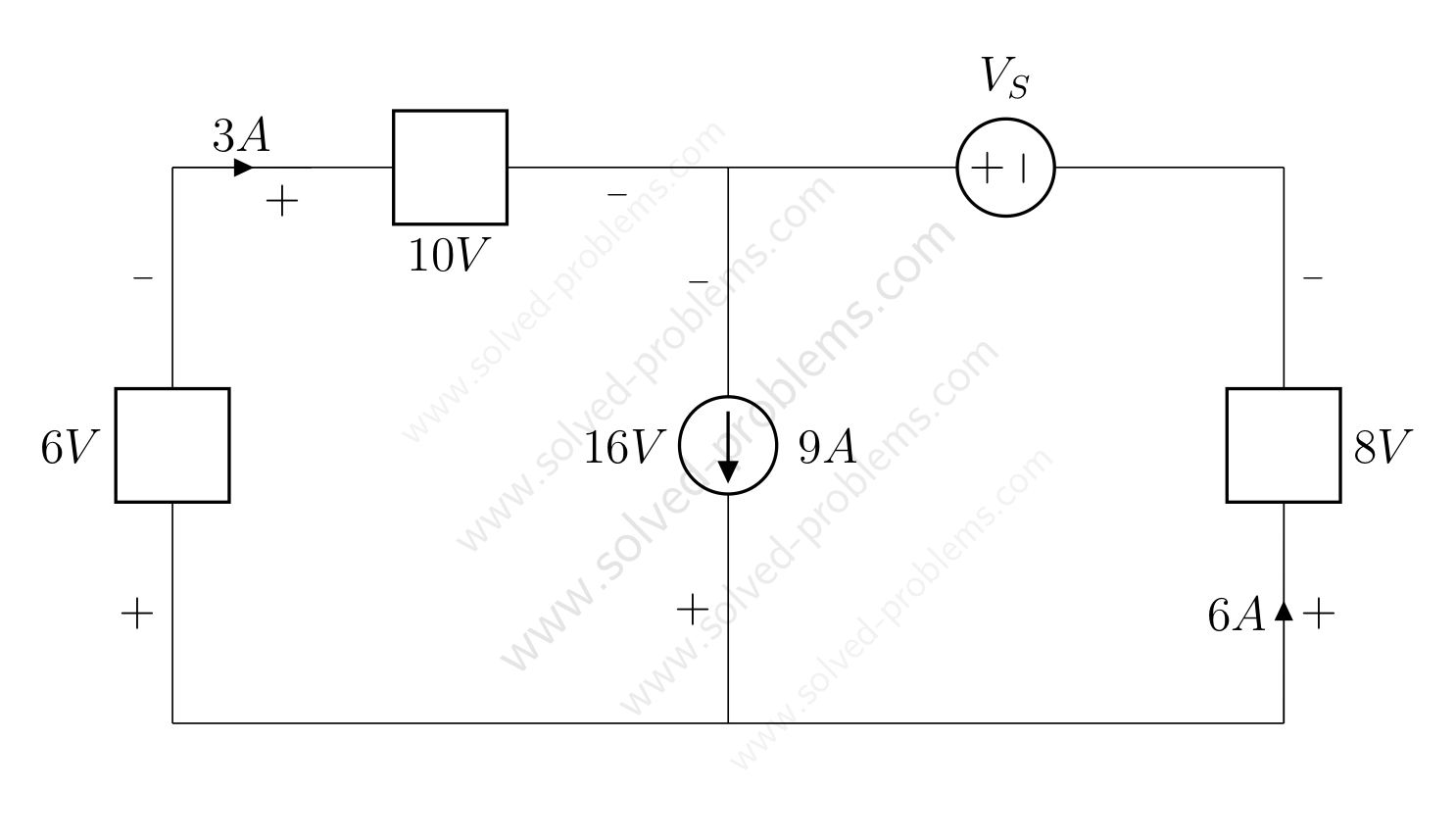
A circuit with two sources and three two port elements is studied. Some voltages and currents are given. Voltage of the voltage source is unknown. We need to analyze the circuit, find power of other elements and use the energy conservation to determine the power of the voltage source.
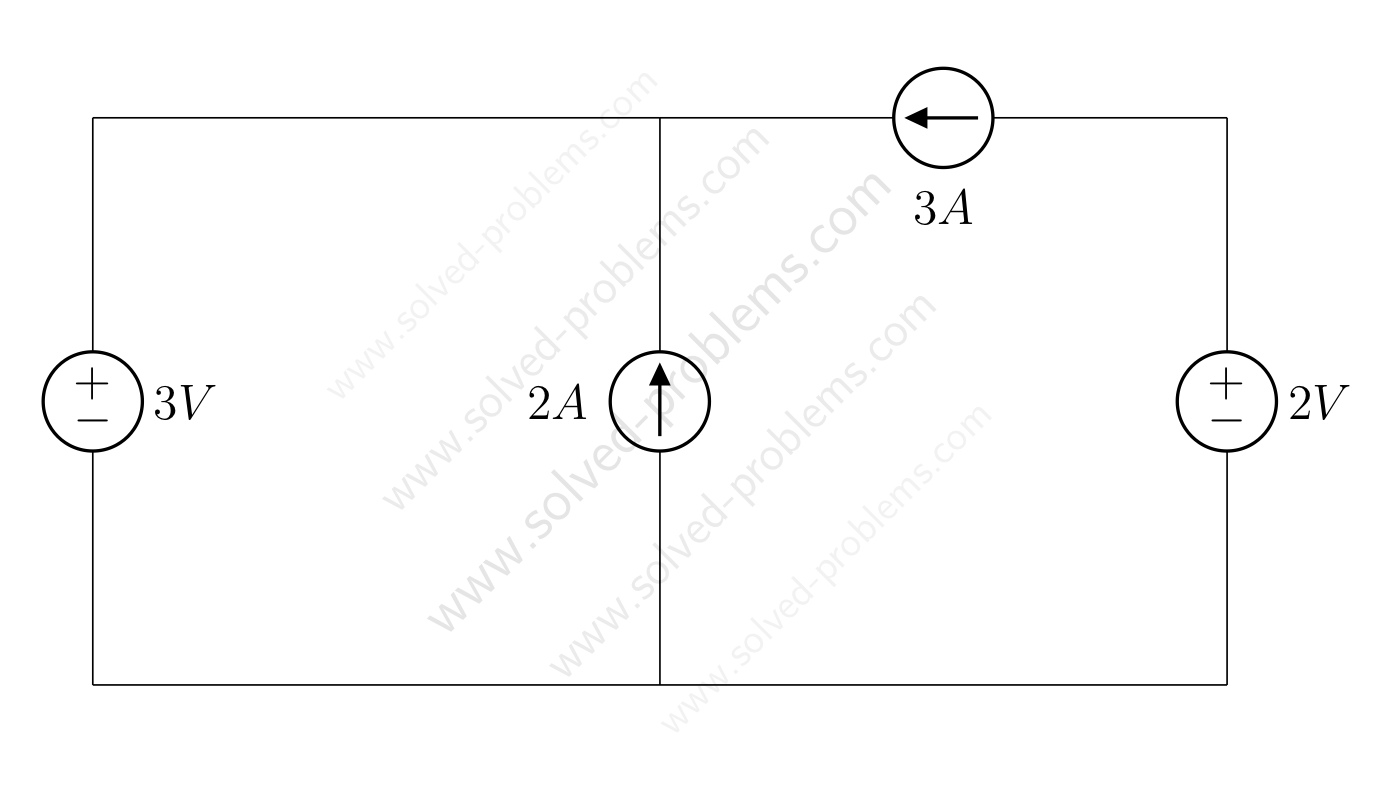
Circuit Containing Only Sources
We go through solving a circuit which only containes independent sources: two voltage sources and two current sources. KVL and KCL are used to determine voltages and currents.
Find the current using superposition.
Superposition rule is used to solve a DC resistive circuit which has two independent voltage sources and four resistors.
AC Circuit Analysis – Sources with Different Frequencies
In AC circuit analysis, if the circuit has sources operating at different frequencies, Superposition theorem can be used to solve the circuit. Please note that AC circuits are linear and that is why Superposition theorem is valid to solve them. Problem Determine where and . Solution with AC Circuit Analysis Since sources are operating at …
Continue reading “AC Circuit Analysis – Sources with Different Frequencies”
Mesh (Current) Analysis Problem
A circuit with four meshes solved using the mesh analysis. The circuit has two current sources, one voltage source and six resistors.
Winner of Electrical Circuits Contest #1
Problem Find and : Solution Three resistors are in series and their equivalent, , is parallel with the voltage source. So, according to the Ohm’s law: . The negative sign comes from the direction . Applying KCL at the bottom node: . The lucky winner of the Electrical Circuits Contest #1 is Kunal Marwaha from …
Find Equivalent Impedance – AC Steady State Analysis
Determine the driving-point impedance of the network at a frequency of kHz: Solution Lets first find impedance of elements one by one: Resistor The resistor impedance is purely real and independent of frequency.
Electrical Circuit Contest – Win $10!
What’s up? We are going to have fun! This is our first contest for electrical circuits. Solve the problem, submit your answers and cross your fingers to be the lucky winner! Problem Find and :
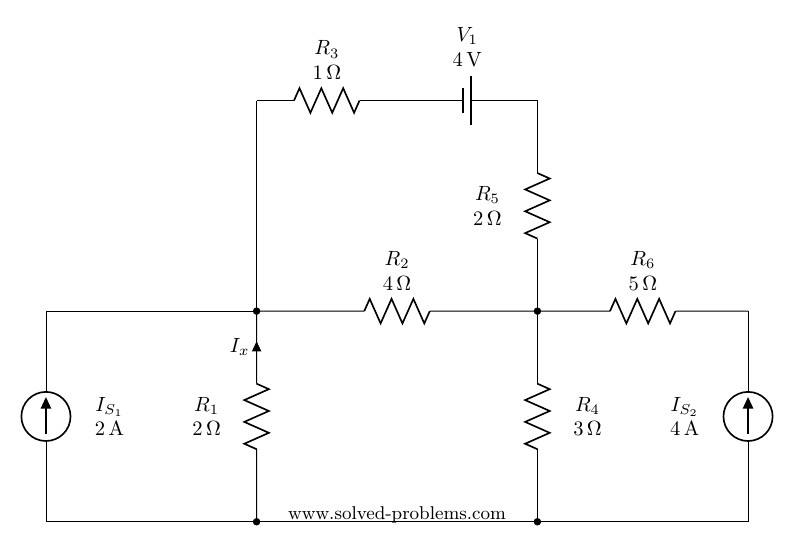
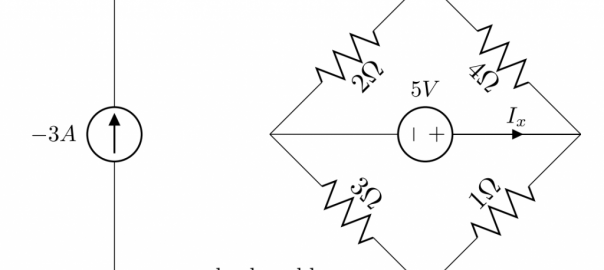
Superposition method – Circuit with two sources
Finding current by using superposition method. There are two independent sources, so we need to turn them off one by one and calculate their contributions.