Solved Problems

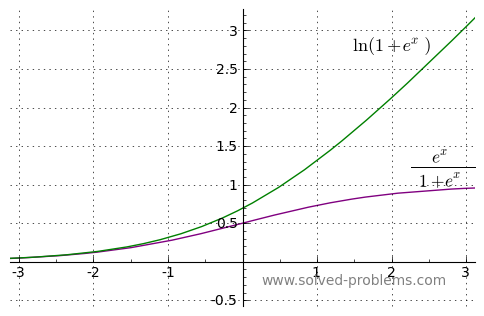
Problem 2-8: Integration

Written by

Yaz

in

,

Find \displaystyle\int \! \frac{e^x}{1+e^x}\, dx.

Solution

Let u=1+e^x, therefore du=e^x dx \to dx=\frac{1}{u-1}du. Hence

\displaystyle\int \! \frac{e^x}{1+e^x}\, dx = \displaystyle\int \! \frac{u-1}{u} \frac{1}{u-1}\,du = \displaystyle\int \! \frac{1}{u} \,du=\ln (u)=\ln(1+e^x)
Problem 2-8

Comments

3 responses to “Problem 2-8: Integration”

  1. jose flaminio tellez abril Avatar
    jose flaminio tellez abril

    aprender a integrar


    _____________
    learned to integrate

    Reply
  2. yohannes berhanu Avatar
    yohannes berhanu

    i really appreciate if u can send me newsletter every week. i am a pre college student , and i am glad to have this kind of website that would enable me and other fellas to succed on their academic activities.

    Reply
    1. Dr. Yaz Z. Li Avatar
      Dr. Yaz Z. Li

      Dear Yohannes,

      I am thinking of starting a newsletter. All registered user would be receiving it.

      Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

More posts