Solved Problems

Tag: Superposition

  • Find the current using superposition.

    Find the current using superposition.

    Find the current passing through the 2Ω resistor using superposition.

    (more…)
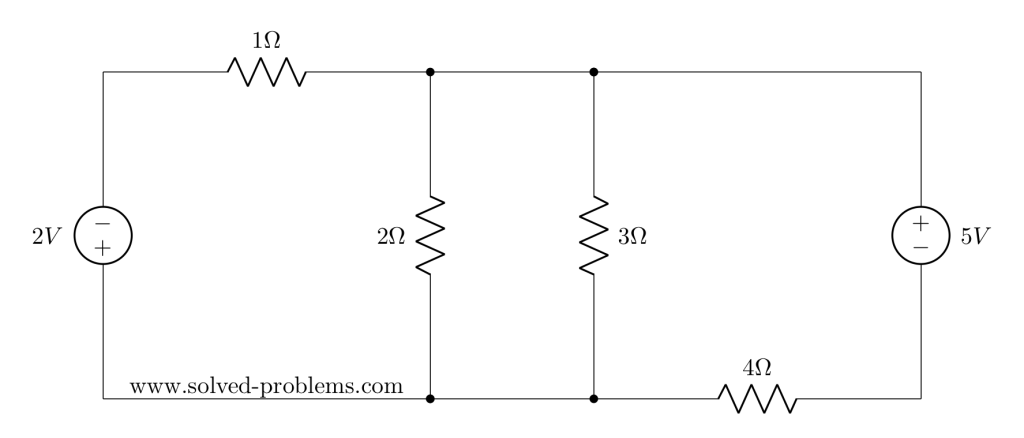
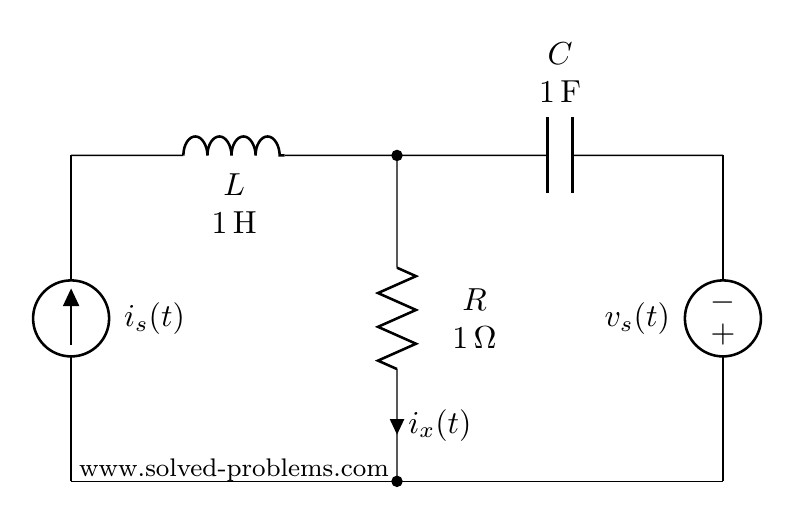
  • AC Circuit Analysis – Sources with Different Frequencies

    AC Circuit Analysis – Sources with Different Frequencies

    In AC circuit analysis, if the circuit has sources operating at different frequencies, Superposition theorem can be used to solve the circuit. Please note that AC circuits are linear and that is why Superposition theorem is valid to solve them.

    Problem

    Determine i_x(t) where i_s(t)=4 \cos (4t) ~ A and v_s(t)=2 \sin (2t) ~ V.
    ac circuit analysis with different source frequencies

    Solution with AC Circuit Analysis

    Since sources are operating at different frequencies, i.e. 4 \frac{rad}{s} and 2 \frac{rad}{s}, we have to use the Superposition theorem. That is to say that we need to determine contribution of each source on i_x(t). Then, the final answer is to obtained by adding the individual responses in the time domain. Please note that, since the impedances depend on frequency, we need to have a different frequency-domain circuit for each frequency.

    Contribution of the current source

    To find the contribution of the current source, we need to turn off other source(s). So, we need to turn off the voltage source. This is very similar to DC circuits that we discussed before:

    Voltage sources become a short circuit when turned off.

    Turning off the voltage source for AC steady state circuit problem containing sources with different frequencies

    Frequency domain

    We first convert the circuit to the frequency domain:
    i_s(t)=4 \cos (4t) ~ A \rightarrow I_s=4\angle 0^{\circ} (\omega = 4 \frac{rad}{s})
    L=1\text{H} \rightarrow Z_L=j \omega L=j4
    C=1\text{F} \rightarrow Z_C=\frac{1}{j \omega C}=\frac{1}{j4}=-j0.25
    R=1 \Omega \rightarrow Z_R=R=1
    i_{x_1}(t) \rightarrow I_{x_1}

    Using current divider:
    I_{x_1}=\frac{Z_C}{Z_C+R}I_s
    =\frac{-j0.25}{-j0.25+1} \times 4
    =\frac{-j0.25}{1-j0.25} \times 4
    =\frac{-j0.25 \times (1+j0.25)}{(1-j0.25)\times (1+j0.25)} \times 4
    =\frac{-j0.25 + 0.0625)}{1^2+0.25^2} \times 4
    =\frac{-j0.25 + 0.0625)}{1.0625} \times 4
    =0.235-j0.941
    =0.97\angle -76^{\circ}

    Time domain

    Conversion to time-domain:
    i_{x_1}(t)=0.97 \cos (4t-76^{\circ}) ~ \text{A}
    Please note that the sinusoidal function for i_s(t) is cosine and consequently, cosine must be used in converting I_{x_1} to the time domain.

    Contribution of the voltage source

    To find the contribution of the voltage source, the current source needs to be turned off. As mentioned before:

    To turn off a current source it should be replaced by an open circuit

    Turning off the current source for AC steady state circuit problem containing sources with different frequencies

    Frequency domain

    v_s(t)=2 \sin (2t) ~ V \rightarrow V_s=2\angle 0^{\circ} (\omega = 2 \frac{rad}{s})
    L=1\text{H} \rightarrow Z_L=j \omega L=j2
    C=1\text{F} \rightarrow Z_C=\frac{1}{j \omega C}=\frac{1}{j2}=-j0.5
    R=1 \Omega \rightarrow Z_R=R=1
    i_{x_2}(t) \rightarrow I_{x_2}

    As the inductor branch is open, this is a very simple circuit with three elements in series: R, Z_C and V_s. Therefore,
    I_{x_2}=\frac{V_s}{R+Z_C}
    =\frac{2}{1-j0.5}
    =\frac{2\times (1+j0.5)}{(1-j0.5)\times (1+j0.5)}
    =\frac{2+j}{1^2+0.5^2}
    =\frac{2+j}{1.25}
    =1.6+j0.8
    =1.789\angle 26.6^{\circ}

    Time domain

    i_{x_2}(t)=1.789 \sin (2t+26.6^{\circ}) ~ \text{A}
    (why \sin?)

    Answer

    Now that we have determined both i_{x_1}(t) and i_{x_2}(t) in time domain, we can go ahead and add them up to find i_x(t). Please note that we could not add I_{x_1} and I_{x_2} because they are not phasors with the same frequency.
    i_{x}(t)=i_{x_1}(t)+i_{x_2}(t)=0.97 \cos (4t-76^{\circ}) + 1.789 \sin (2t+26.6^{\circ}) ~ \text{A}
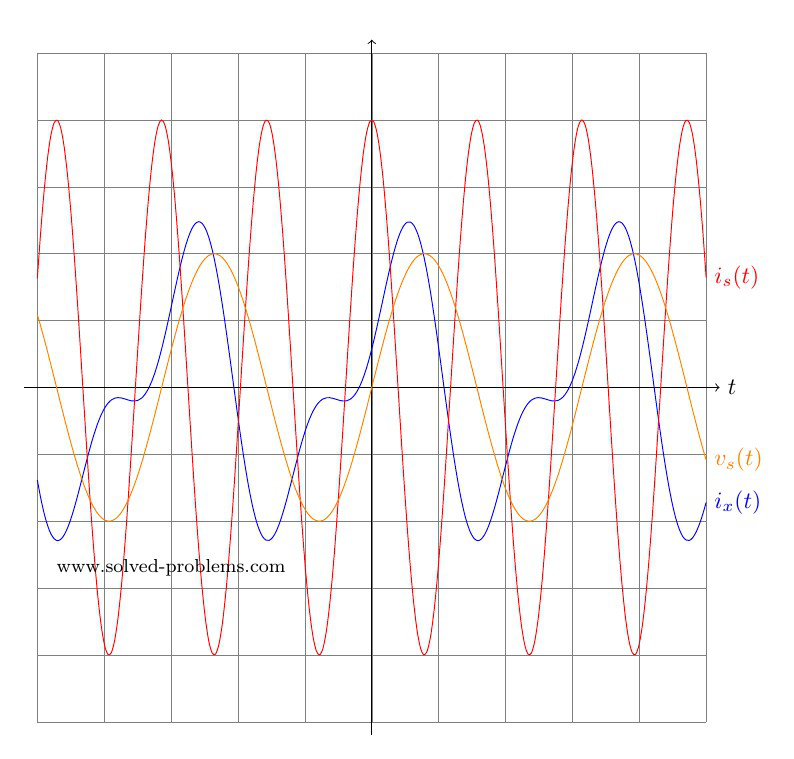
    signal plots - AC Circuit Analysis with superposition theorem

  • Superposition method – Circuit with two sources

    Superposition method – Circuit with two sources

    Find I_x using superposition rule:
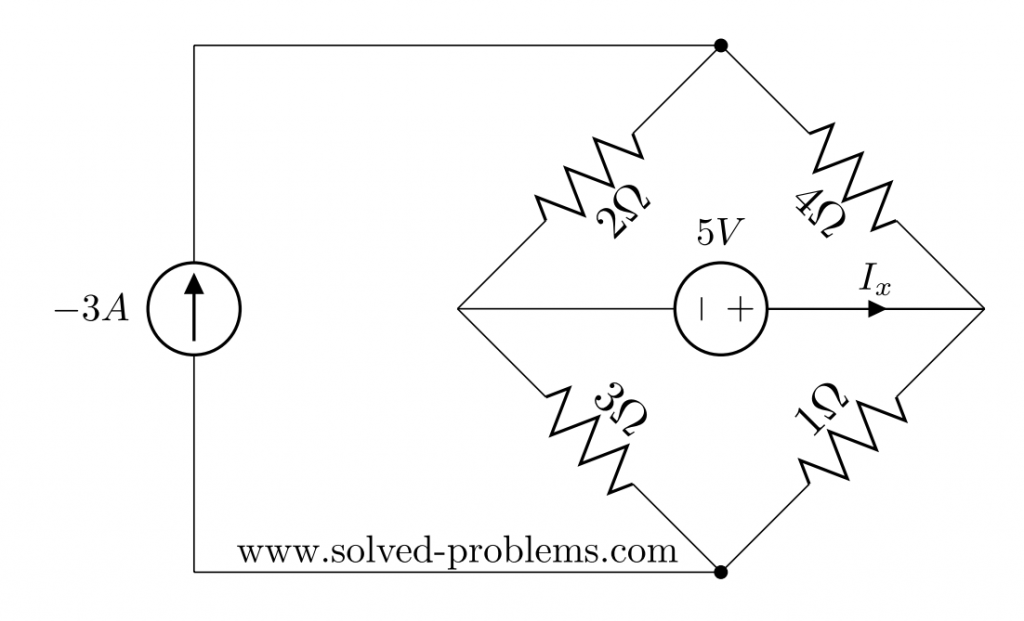
    Main cuircuit to be analyzed using superposition method

    Solution

    Superposition

    The superposition theorem states that the response (voltage or current) in any branch of a linear circuit which has more than one independent source equals the algebraic sum of the responses caused by each independent source acting alone, while all other independent sources are turned off (made zero).
    (more…)

  • Superposition Method – Circuit With Dependent Sources

    Superposition Method – Circuit With Dependent Sources

    Determine I_x , I_y and V_z using the superposition method.

    Superposition - Circuit with dependent sources

    Solution
    I. Contribution of the -2V voltage source:
    We need to turn off the current source by replacing it with an open circuit. Recall that we do not turn off dependent sources. The resulting circuit is shown below.
    (more…)

  • Superposition Problem with Four Voltage and Current Sources

    Superposition Problem with Four Voltage and Current Sources

    Determine V_x and I_x using the superposition method.
    A circuit with four voltage and current sources to be solved by the superposition method
    Solution
    I. Contribution of the -5V voltage source:

    To find the contribution of the -5V voltage source, other three sources should be turned off. The 3V voltage source should be replaced by short circuit. The current source should be replaced with open circuits, as shown below.
    (more…)

  • Turning Sources Off

    Turning Sources Off

    Turning off a source, which is usually used in solving circuits with superposition method, means setting its value equal to zero. For a voltage source, setting the voltage equal to zero means that it produces zero voltage between its terminals. Therefore, the voltage source must insure that the voltage across two terminals is zero. Replacing the source with a short circuit can do that. Thus, voltage sources become a short circuit when turned off.

    For a current source, setting the current equal to zero means that it produces zero current. Therefore, the current source must insure that no current flows through its branch. An open circuit can do that. Hence, to turn off a current source it should be replaced by an open circuit.

    How about dependent sources? The voltage/current of a dependent source is dependent on other variables of the circuit. Therefore, dependent sources cannot be turned off.

    Example I: Turn off sources one by one.

    turning sources off example 1-1
    Example 1

    Solution:
    I) The voltage source:

    turning sources off example 1-2
    Turning off the voltage source

    (more…)