Deploy nodal analysis method to solve the circuit and find the power of the dependent source.
I. Identify all nodes in the circuit.
The circuit has 4 nodes.
Tag: Power
-
Nodal Analysis – Dependent Current Source
-
Nodal Analysis – Five-Node Circuit
Use nodal analysis to solve the circuit shown below and determine the power of node
.
I. Identify all nodes in the circuit.
(more…)
The circuit has five nodes as shown below. -
Mesh Analysis – Supermesh
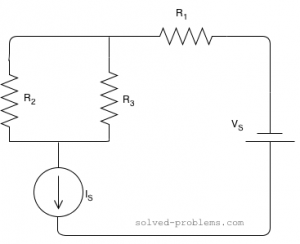
Solve the circuit and find the power of sources:
, 
, 
, 
, 
, 
.Solution:
There are three meshes in the circuit. So, we need to assign three mesh currents. It is better to have all the mesh currents loop in the same direction (usually clockwise) to prevent errors when writing out the equations.
(more…) -
Problem 1-15: Power of Independent Sources
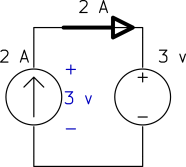
Determine the power of each source.
a)
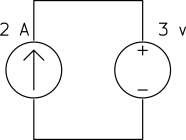
b)
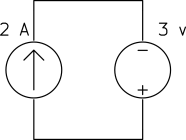
Solution
a) The current source keeps the current of the loop
and the voltage source keeps the voltage across the current source 
as shown below.
(more…) -
Problem 1-8: Nodal Analysis – Power of Current Source
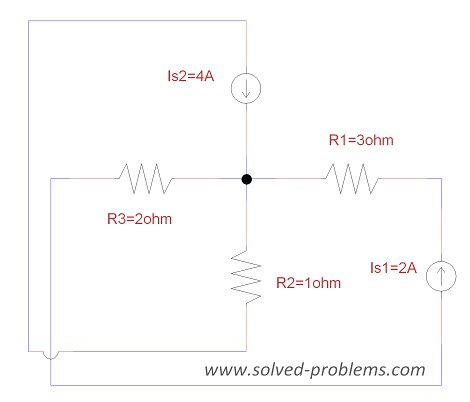
Solve the circuit using nodal analysis and find the power of
.
Solution
a) Choose a reference node, label the voltages:
(more…) -
Problem 1-1: Power of Elements
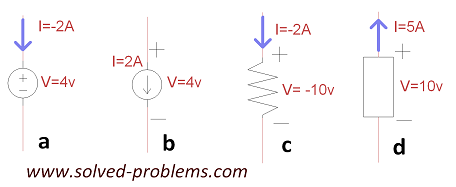
Find the power of each element. Which one is supplying power and which one is absorbing it?
Solution
a) Passive sign convention,
supplying power.
(more…)
and power absorbed or supplied by each element.
and 
.
.