Solve the circuit using nodal analysis and find the power of ![]() .
.
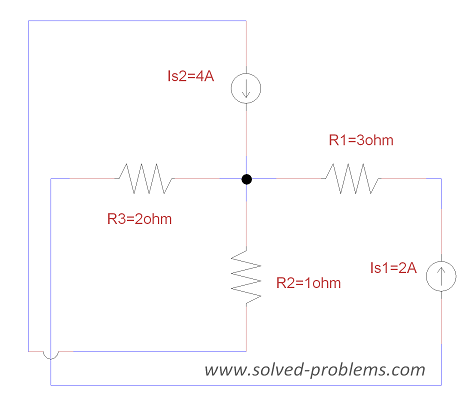
Solution
a) Choose a reference node, label the voltages:
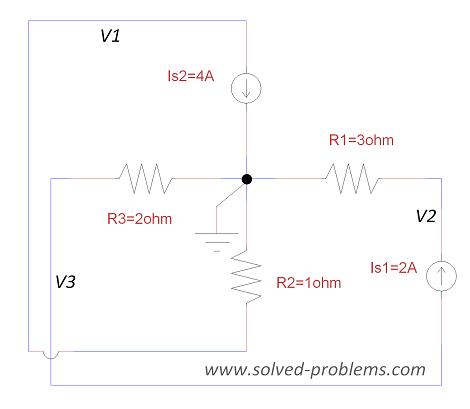
b) Apply KCL to nodes:
Node #1:
![]()
Node #2:
![]()
Node #3:
![]() .
.
c) Find the unknown:
![]() supplying.
supplying.
Solve the circuit using nodal analysis and find the power of ![]() .
.

Solution
a) Choose a reference node, label the voltages:

b) Apply KCL to nodes:
Node #1:
![]()
Node #2:
![]()
Node #3:
![]() .
.
c) Find the unknown:
![]() supplying.
supplying.
Can we ignore R2-Is2 loop and say that R1 and R3 are in series so R13=5ohm and the power is RI^2=5*2^2=20W?
Yes, it is ok to ignore the ![]() –
– ![]() loop because it has only one common point with the other loop and current cannot flow between. Your solution is also correct.
loop because it has only one common point with the other loop and current cannot flow between. Your solution is also correct.
I got 20W for the answer. How do you know if it is negative or positive? I know SRS, however I am not sure of how to apply it in this problem. Where do the plus and minus go?
Leave a Reply