Find I_9 (Hint: use circuit reduction).
All resistors are 10\Omega and Is_1=10A
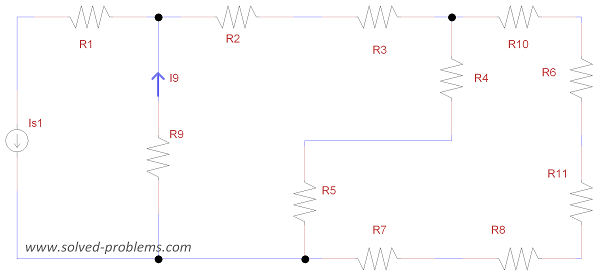
Problem 1-7 - Circuit Reduction

Solution
Let’s redraw the circuit:


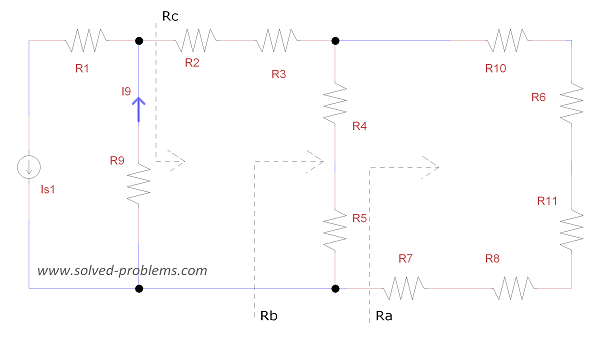
Circuit Reduction - Redrawing the circuit
The equivalent resistances are: R_a= R_{10}+R_6+R_{11}+R_8+R_7=50 \Omega

R_b= R_a ||(R4+R_5)=50 || 20 = \frac{100}{7} \Omega

R_c= R_b+R_2+R_3=\frac{240}{7} \Omega

Now, the circuit is reduced to:
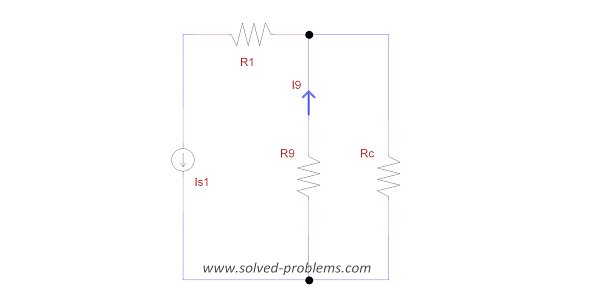
Circuit Reduction - Reduced circuit
Using current divider:

I_9=\frac{R_c}{R_9+R_c} \times Is_1= 7.742 A

Published by Yaz

Hi! Yaz is here. I am passionate about learning and teaching. I try to explain every detail simultaneously with examples to ensure that students will remember them later too.

Join the Conversation

5 Comments

  1. In this case (r2+r3)//(r4+r5).. so why cant we apllly the current divider rule to this.???
    please explain…

    Reply

    1. Those two branches are not in parallel. They would be parallel if R9 was a short circuit. So, if you replace R9 with a short circuit, Rnew=(R2+R3)||(R4+R5) with one node connected to the left node of R10 and the another one connected to the left of R7.

      Reply
      1. Reply
  2. Reply

  3. In Using current divider: of Problem 1-7: Circuit Reduction – Current Divider
    Posted byYaz April 15, 2010

    I9=Rc / R9+Rc × Is1 = 7.742A there is a typo the first Rc should be R9 as numerator.

    Reply

Leave a comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.