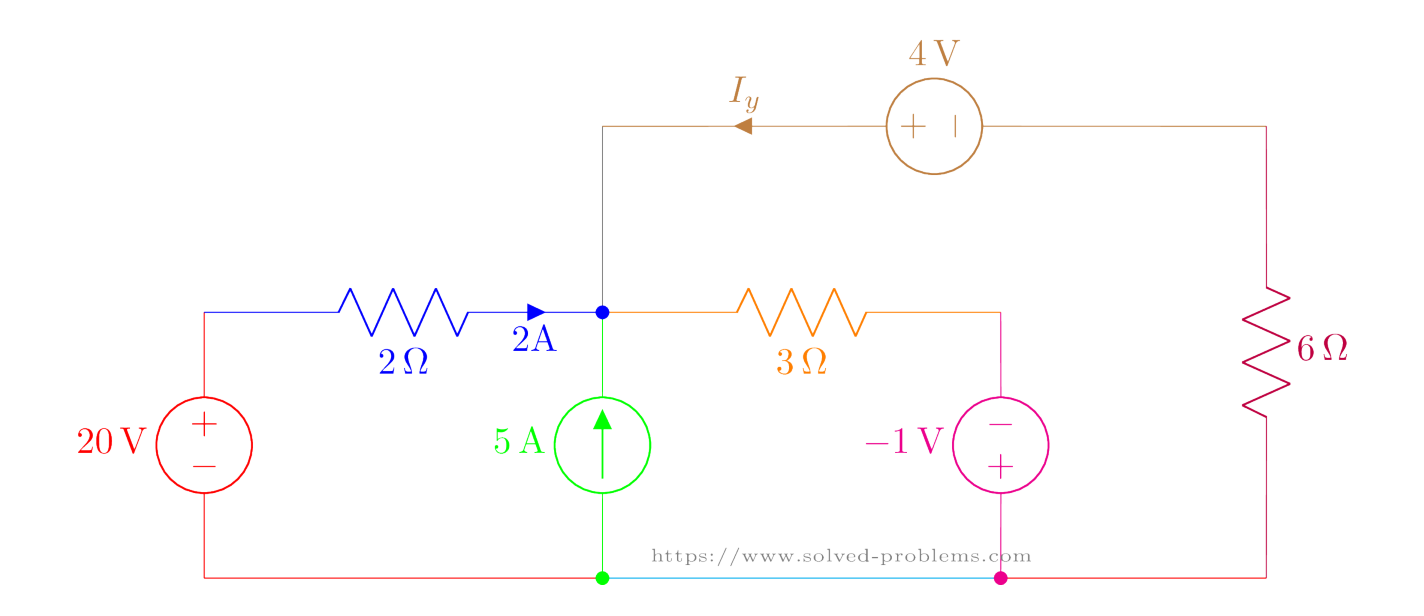
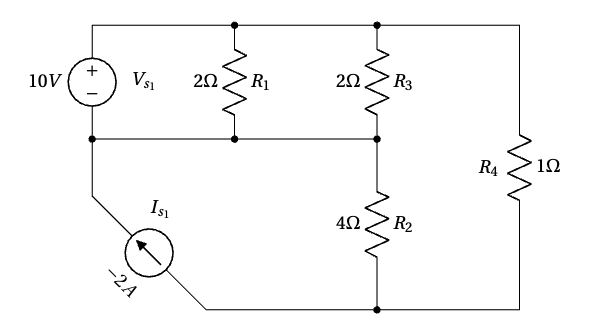
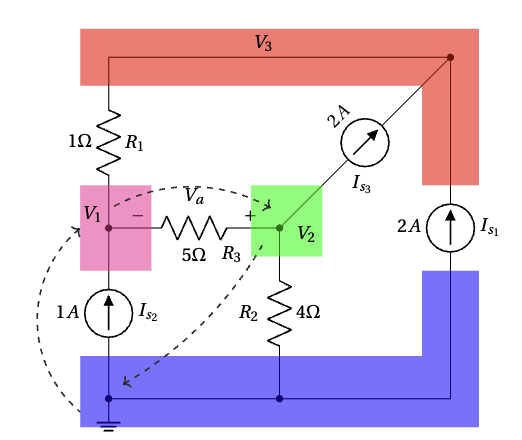
Use Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL) to find ![]() and
and ![]() .
.
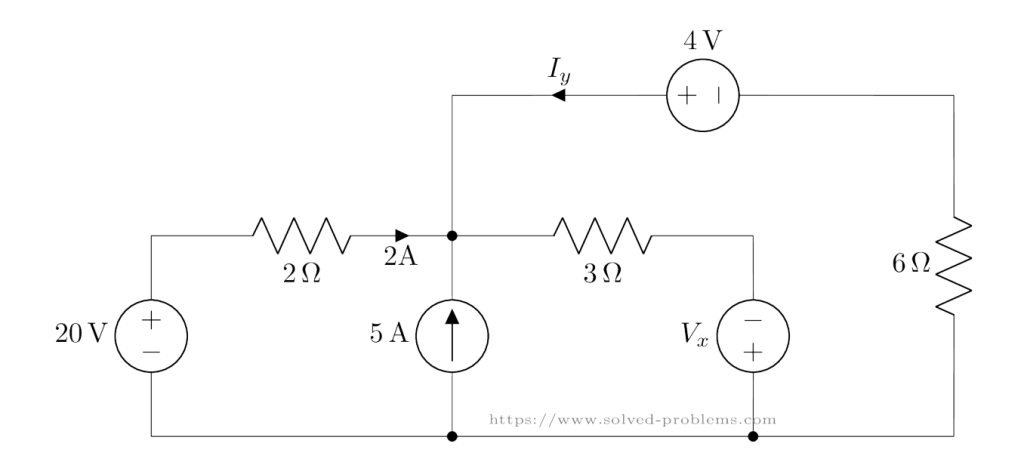
Applying Kirchhoff’s Voltage Law (KVL)
KVL states: The sum of all voltages in a closed loop is zero.
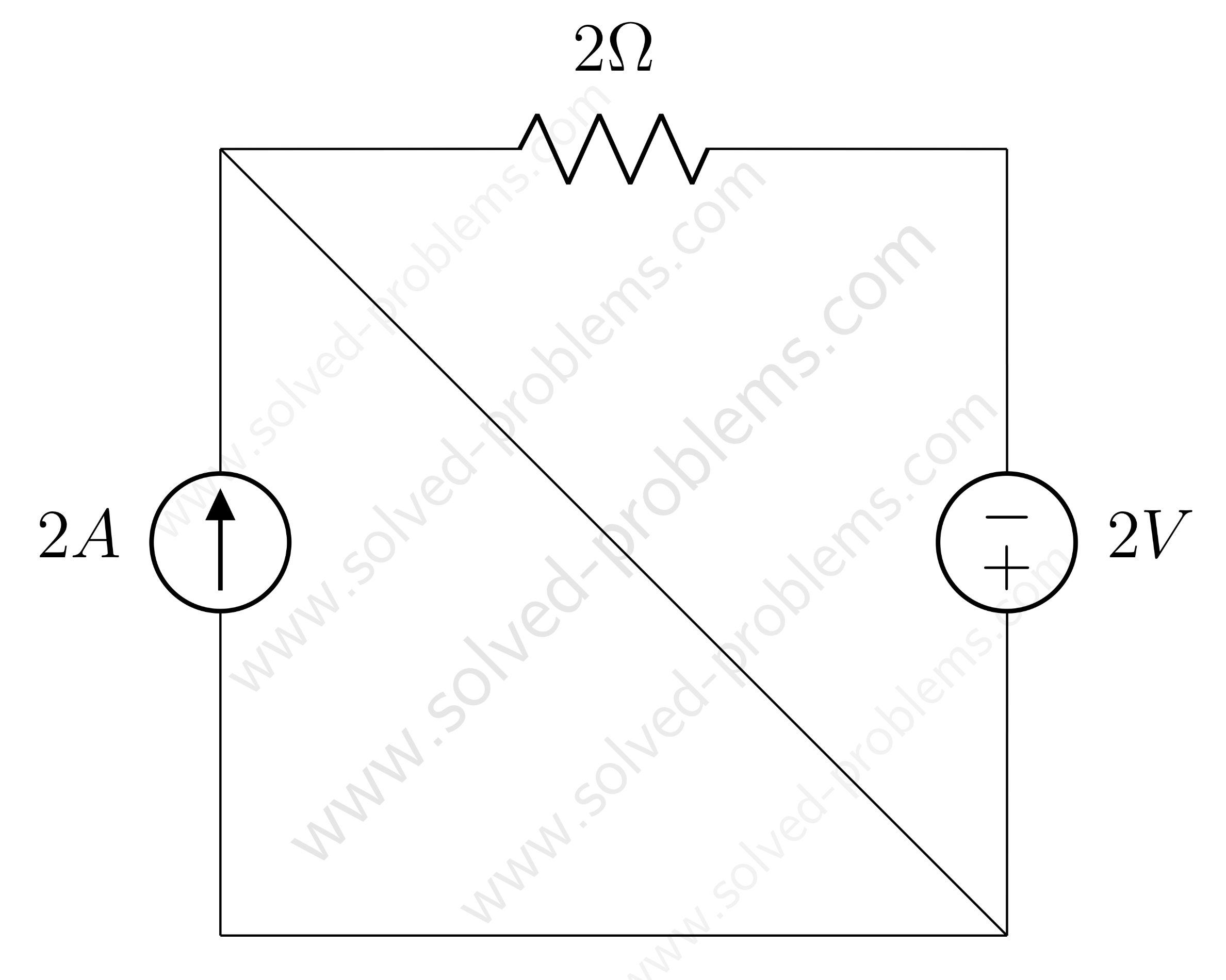
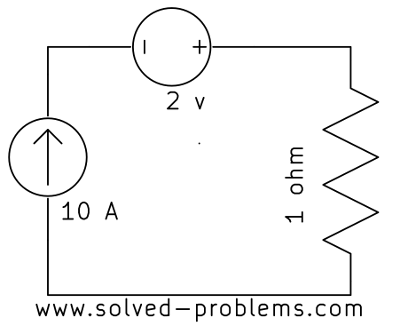
Loop 1: 20V Source, 2Ω Resistor, and 5A Current Source
We start with Loop 1 which is shown below.
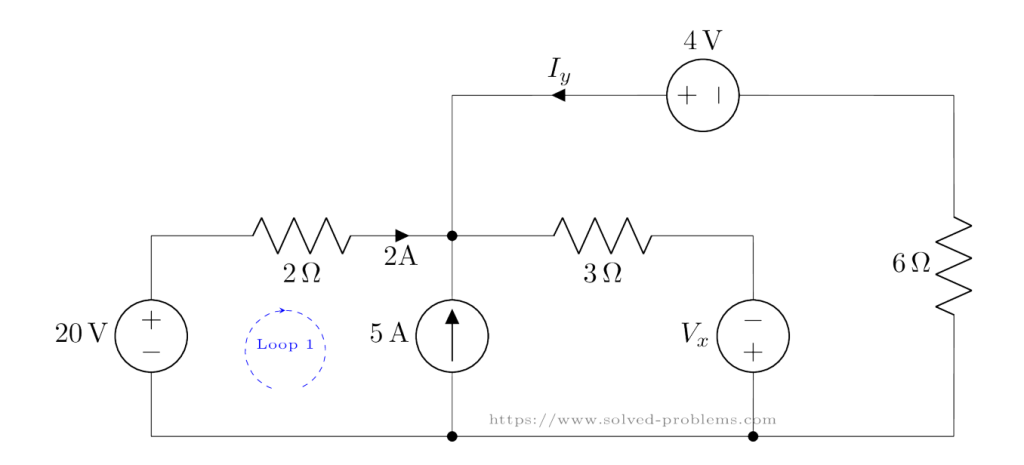
The KVL equation is:
![]()
Simplify:
![]()
![]()
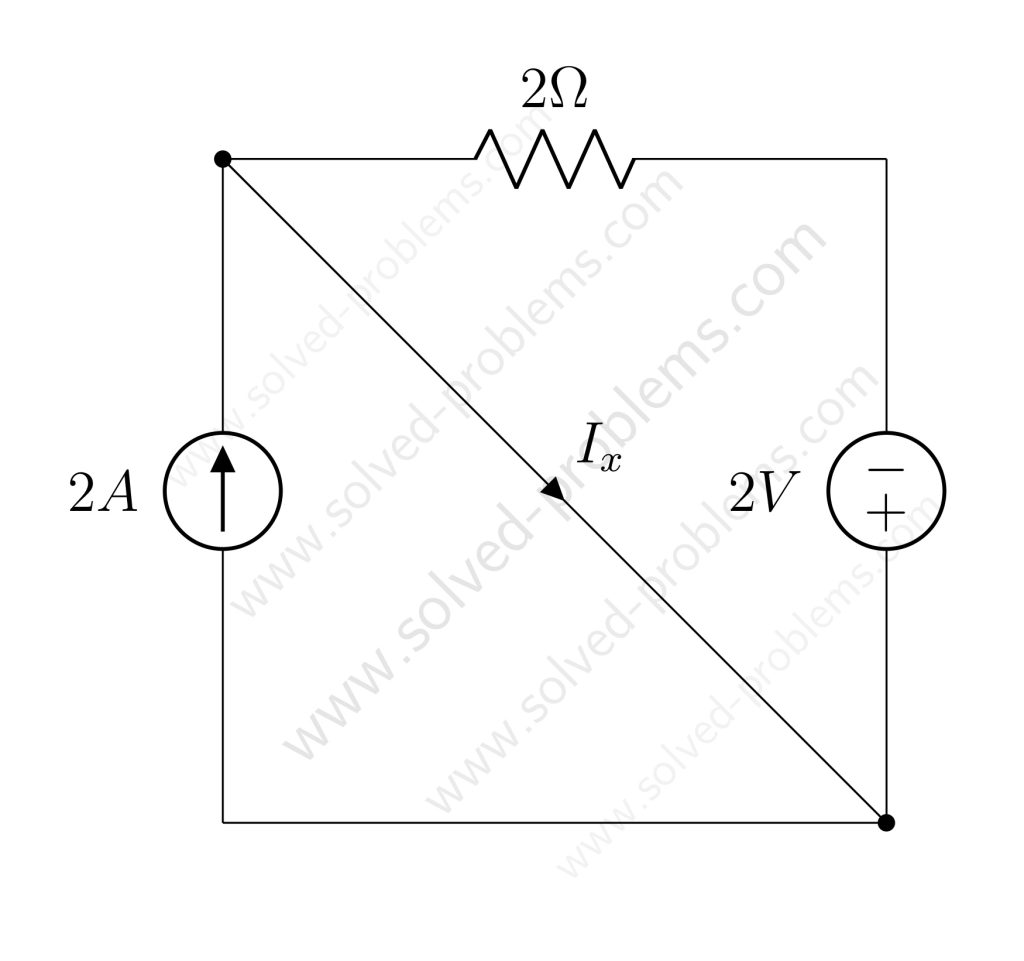
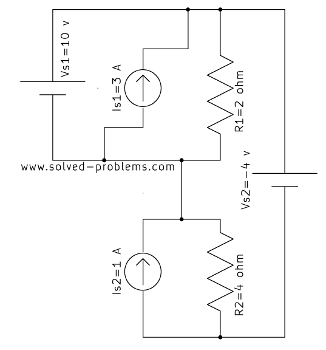
Loop 2: Voltage Across![]() , 3V Source, and 7Ω Resistor
, 3V Source, and 7Ω Resistor
Next, we analyze Loop 2 shown below:
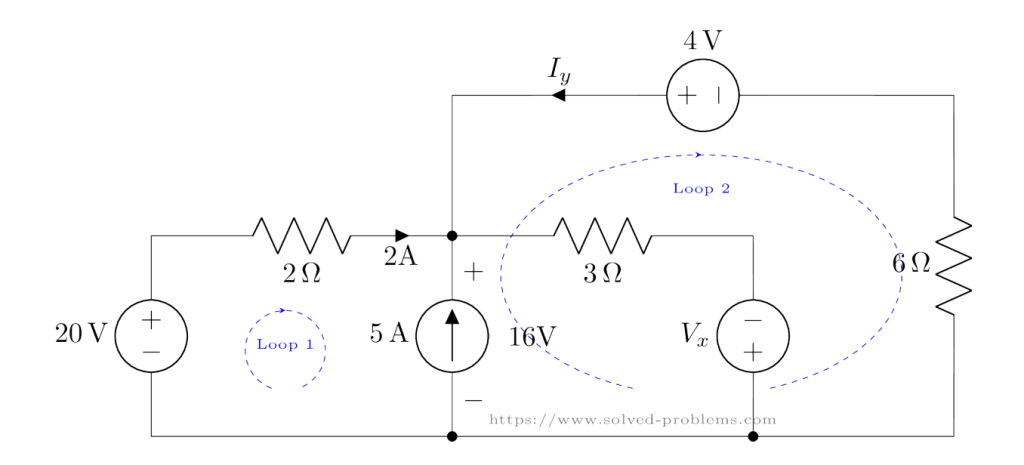
The equation is:
![]()
Simplify:
![]()
![]()
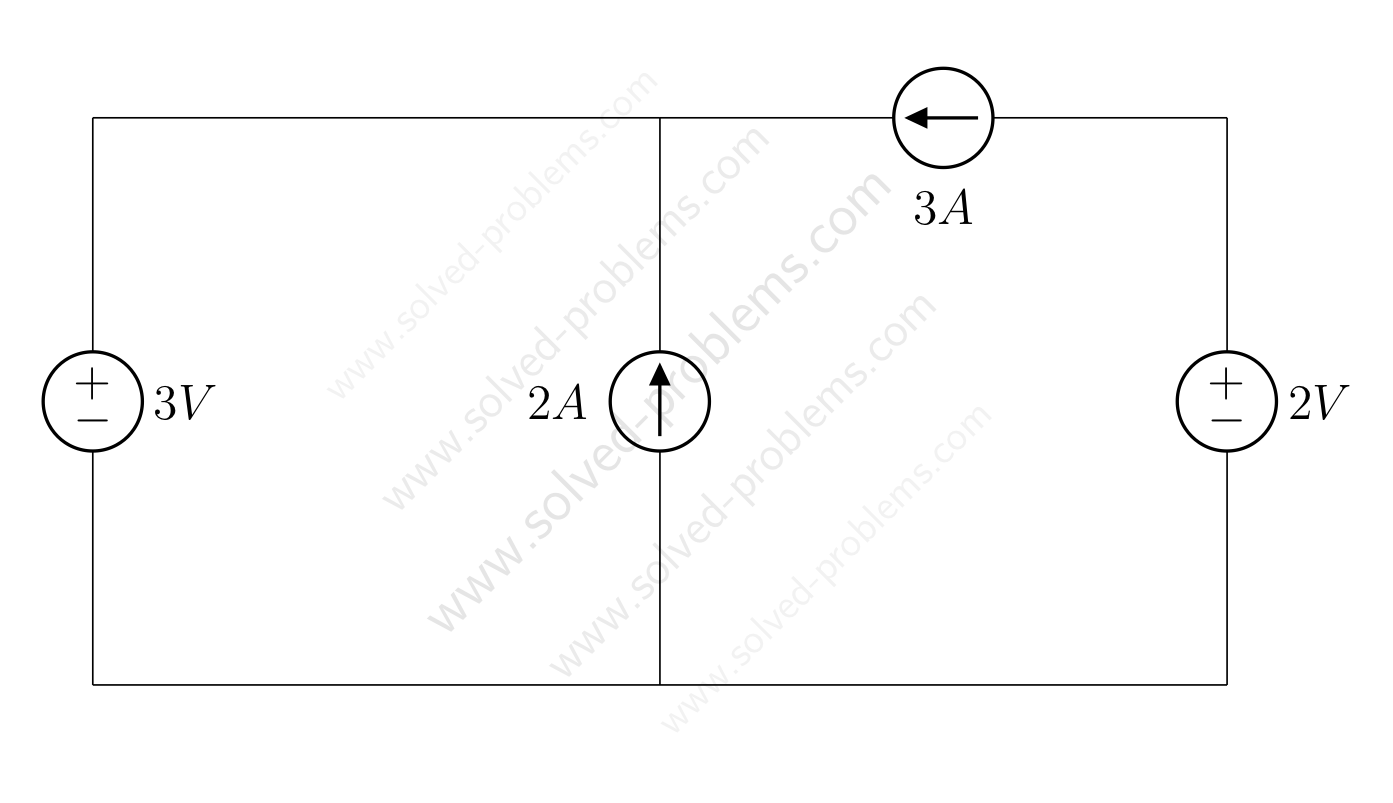
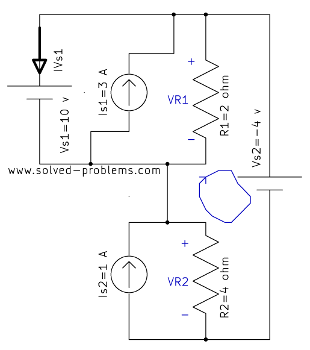
KCL: Applying Kirchhoff’s Current Law (KCL)
KCL states: The total current entering a node equals the total current leaving the node.
At the middle node, the currents are:
![]()
Simplify:
![]()
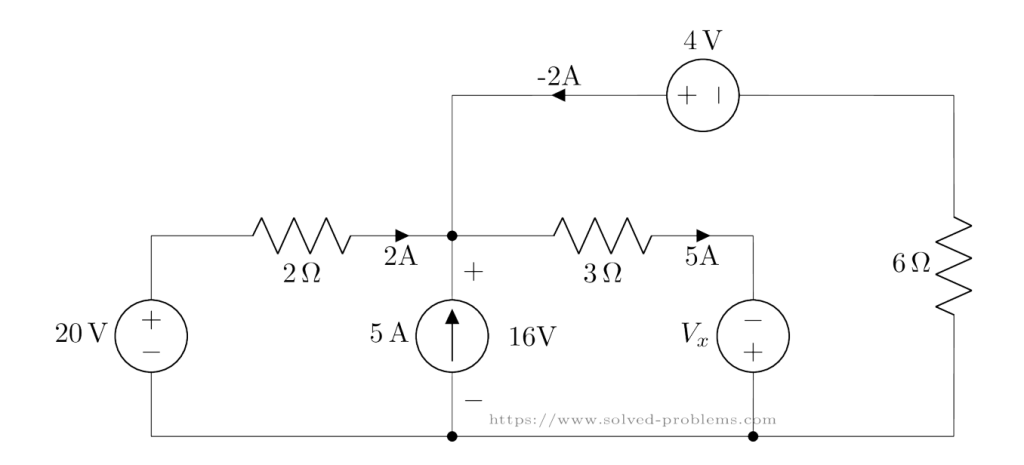
Finding ![]()
Finally, we calculate ![]() using KVL in Loop 3:
using KVL in Loop 3:
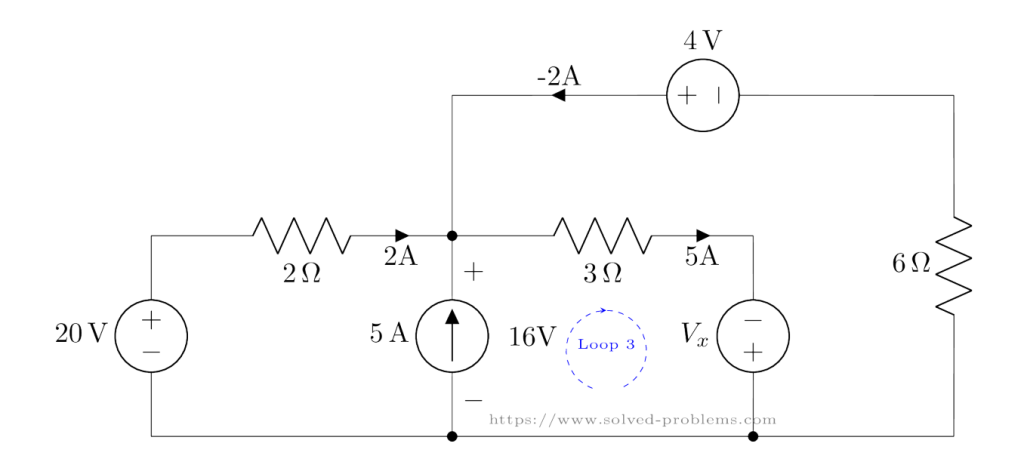
The equation is:
![]()
Simplify:
![]()
![]()
Using Python to Solve the Circuit
One powerful way to solve electrical circuits is by using the Lcapy library in Python. Lcapy is an open-source Python package designed for symbolic linear circuit analysis and signal processing.
Below is an example of how to use Lcapy to solve the given circuit and find ![]() (the current through
(the current through ![]() ) and
) and ![]() (the current through the 2Ω resistor).
(the current through the 2Ω resistor).
—
Python Code to Solve the Circuit
```python
from lcapy import Circuit
cct = Circuit("""
V1 1 0 20; down,
R1 1 N_A 2; right=1.5, i=I_{R_1},
I1 N_A 0_2 5; down,
W N_A 5; up=0.7,
R2 N_A 3 3; right=1.5,
V_x 0_3 3 -1; up,
V2 5 4 4; right=2, i=I_y,
R4 0_4 4 6; up,
W 0 0_2; right,
W 0_2 0_3; right,
W 0_3 0_4; right,
""")
print(f"Current through R1 (I_R1): {cct.R1.i}")
print(f"Current through V2 (I_y): {cct.V2.i}")which prints
Current through R1 (I_R1): 2
Current through V2 (I_y): -2