Which one of the following functions are even or odd or neither?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Recall that a function is said to be even if ![]() and odd if
and odd if ![]() .
.
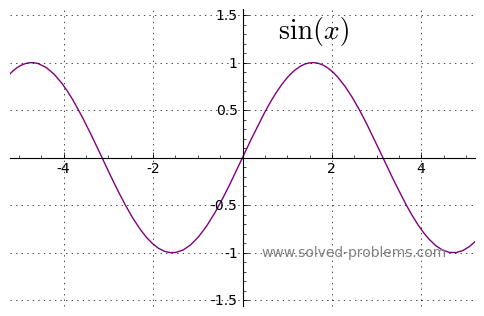
Solution
a) Odd ![]()
b) Even ![]()
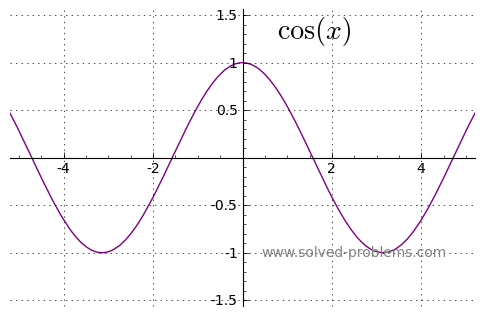
c) Odd ![]()
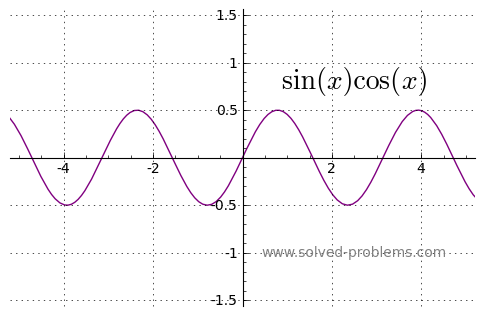
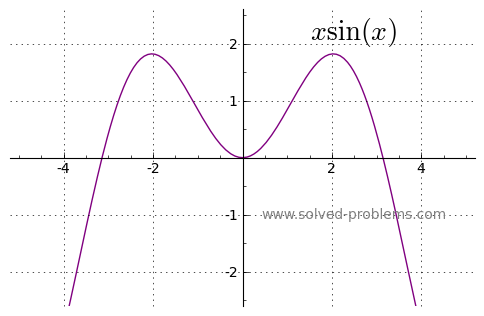
d) Even ![]()
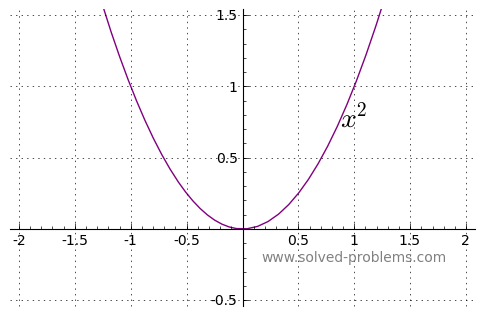
e) Even ![]()
f) Neither ![]()
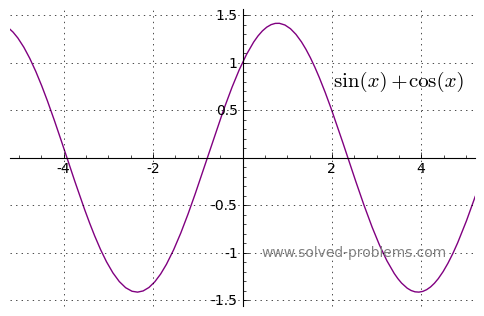
Which one of the following functions are even or odd or neither?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Recall that a function is said to be even if ![]() and odd if
and odd if ![]() .
.

Solution
a) Odd ![]()
b) Even ![]()

c) Odd ![]()


d) Even ![]()

e) Even ![]()
f) Neither ![]()

Please can you solve this example
X(t)=u(t-1)-u(t-3)
Express the signal using its even function xe(t) and Odd function xo(t)
Then sketch the original signal
Leave a Reply