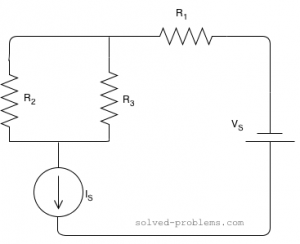
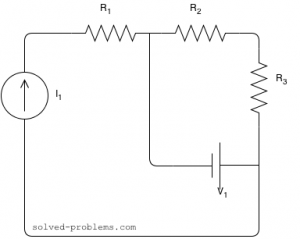
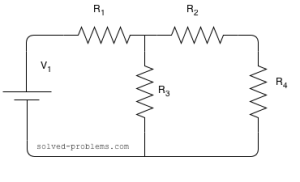
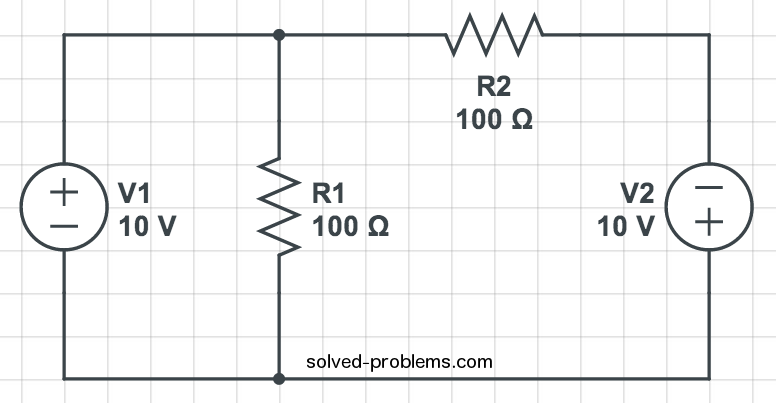
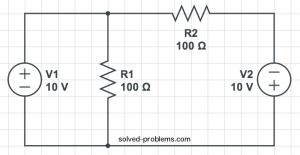
Find Thevenin’s and Norton’s Equivalent Circuits: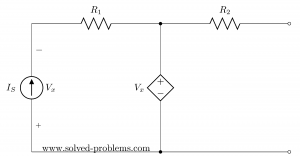
Suppose that ![]() ,
, ![]() and
and ![]() .
.
Solution
The circuit has both independent and dependent sources. In these cases, we need to find open circuit voltage and short circuit current to determine Norton’s (and also Thevenin’s) equivalent circuits.
(more…)