Solved Problems

Author: Yaz

  • Solving a Simple Circuit of Three Elements

    Solving a Simple Circuit of Three Elements

    Solved the circuit to determine I_x and power absorbed or supplied by each element.

    (more…)
  • Power and Energy Conservation

    Power and Energy Conservation

    Is the source Vs in the circuit absorbing or supplying power, and how much?

    (more…)
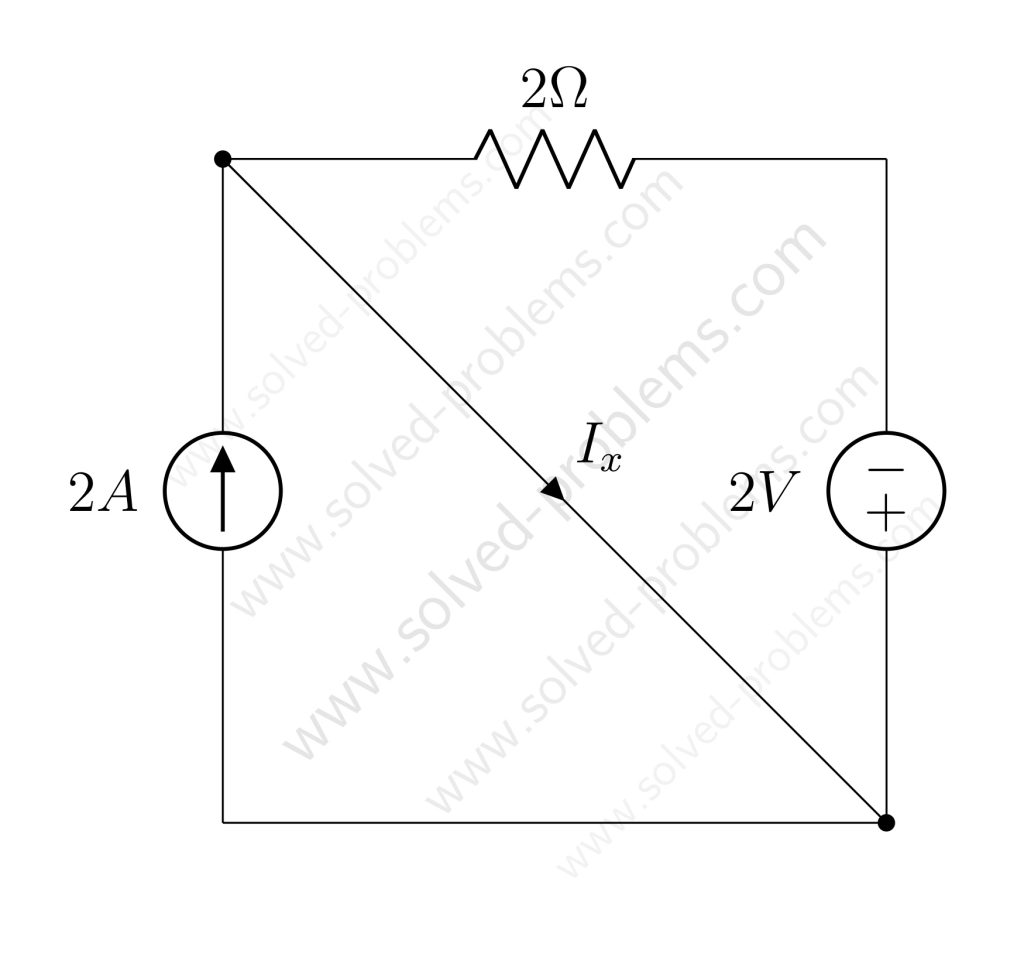
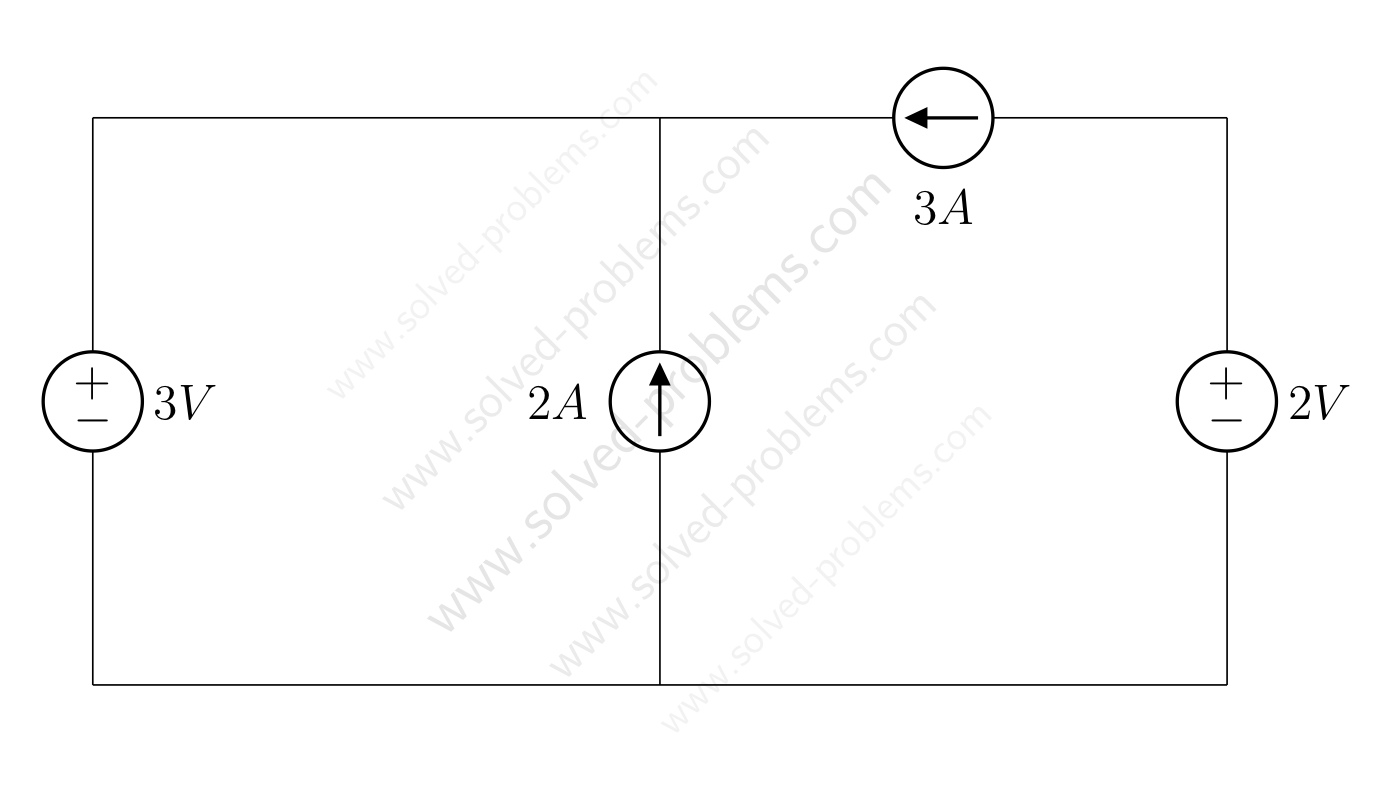
  • Circuit Containing Only Sources

    Circuit Containing Only Sources

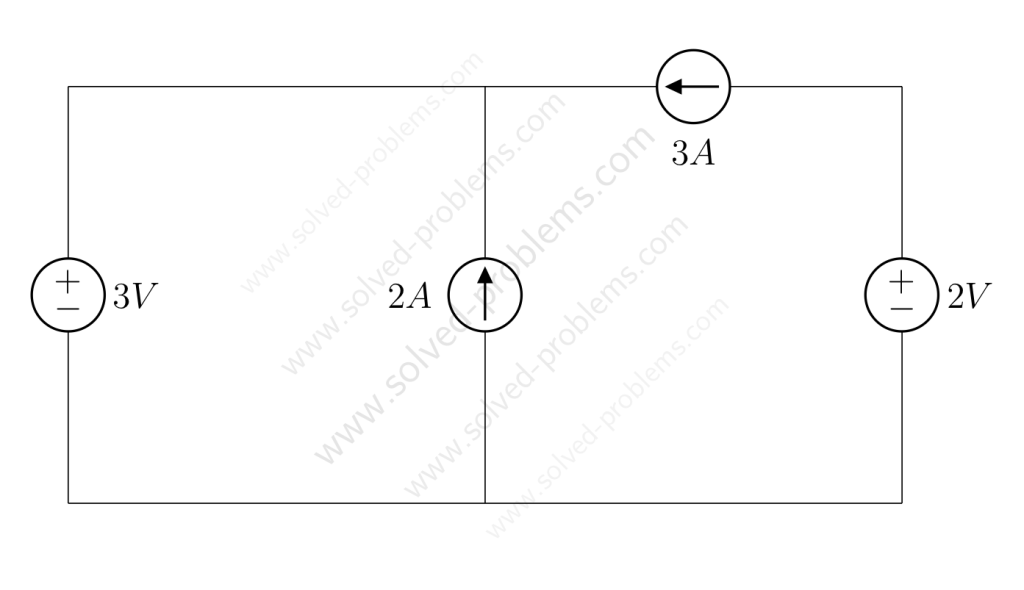
    We go through solving a circuit which only containes independent sources: two voltage sources and two current sources. KVL and KCL are used to determine voltages and currents.

    Determine the amount of power absorbed or supplied by each source.

    (more…)
  • Find the current using superposition.

    Find the current using superposition.

    Find the current passing through the 2Ω resistor using superposition.

    (more…)

  • YouTube Channel

    I started a YouTube channel where is explain how to solve problems. Check it out: https://www.youtube.com/channel/UCE8fpNEhOoHyf78wGGcgwFg
    Here is the first video:

    Please let me know what you think!

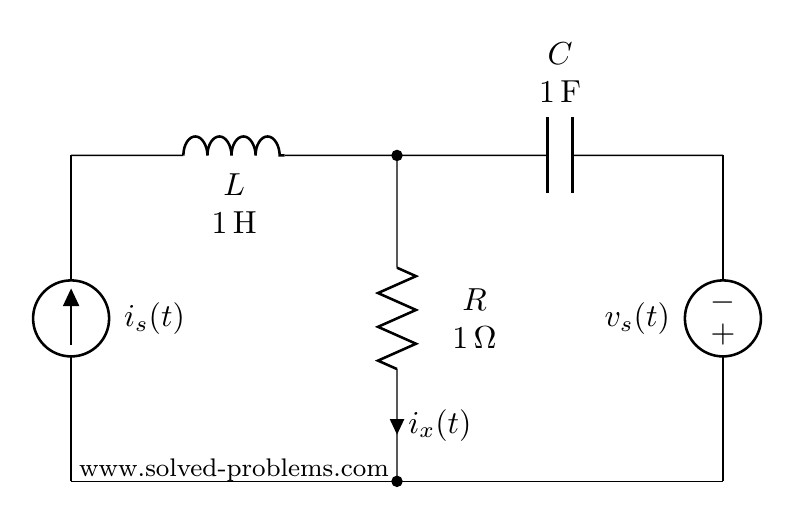
  • AC Circuit Analysis – Sources with Different Frequencies

    AC Circuit Analysis – Sources with Different Frequencies

    In AC circuit analysis, if the circuit has sources operating at different frequencies, Superposition theorem can be used to solve the circuit. Please note that AC circuits are linear and that is why Superposition theorem is valid to solve them.

    Problem

    Determine i_x(t) where i_s(t)=4 \cos (4t) ~ A and v_s(t)=2 \sin (2t) ~ V.
    ac circuit analysis with different source frequencies

    Solution with AC Circuit Analysis

    Since sources are operating at different frequencies, i.e. 4 \frac{rad}{s} and 2 \frac{rad}{s}, we have to use the Superposition theorem. That is to say that we need to determine contribution of each source on i_x(t). Then, the final answer is to obtained by adding the individual responses in the time domain. Please note that, since the impedances depend on frequency, we need to have a different frequency-domain circuit for each frequency.

    Contribution of the current source

    To find the contribution of the current source, we need to turn off other source(s). So, we need to turn off the voltage source. This is very similar to DC circuits that we discussed before:

    Voltage sources become a short circuit when turned off.

    Turning off the voltage source for AC steady state circuit problem containing sources with different frequencies

    Frequency domain

    We first convert the circuit to the frequency domain:
    i_s(t)=4 \cos (4t) ~ A \rightarrow I_s=4\angle 0^{\circ} (\omega = 4 \frac{rad}{s})
    L=1\text{H} \rightarrow Z_L=j \omega L=j4
    C=1\text{F} \rightarrow Z_C=\frac{1}{j \omega C}=\frac{1}{j4}=-j0.25
    R=1 \Omega \rightarrow Z_R=R=1
    i_{x_1}(t) \rightarrow I_{x_1}

    Using current divider:
    I_{x_1}=\frac{Z_C}{Z_C+R}I_s
    =\frac{-j0.25}{-j0.25+1} \times 4
    =\frac{-j0.25}{1-j0.25} \times 4
    =\frac{-j0.25 \times (1+j0.25)}{(1-j0.25)\times (1+j0.25)} \times 4
    =\frac{-j0.25 + 0.0625)}{1^2+0.25^2} \times 4
    =\frac{-j0.25 + 0.0625)}{1.0625} \times 4
    =0.235-j0.941
    =0.97\angle -76^{\circ}

    Time domain

    Conversion to time-domain:
    i_{x_1}(t)=0.97 \cos (4t-76^{\circ}) ~ \text{A}
    Please note that the sinusoidal function for i_s(t) is cosine and consequently, cosine must be used in converting I_{x_1} to the time domain.

    Contribution of the voltage source

    To find the contribution of the voltage source, the current source needs to be turned off. As mentioned before:

    To turn off a current source it should be replaced by an open circuit

    Turning off the current source for AC steady state circuit problem containing sources with different frequencies

    Frequency domain

    v_s(t)=2 \sin (2t) ~ V \rightarrow V_s=2\angle 0^{\circ} (\omega = 2 \frac{rad}{s})
    L=1\text{H} \rightarrow Z_L=j \omega L=j2
    C=1\text{F} \rightarrow Z_C=\frac{1}{j \omega C}=\frac{1}{j2}=-j0.5
    R=1 \Omega \rightarrow Z_R=R=1
    i_{x_2}(t) \rightarrow I_{x_2}

    As the inductor branch is open, this is a very simple circuit with three elements in series: R, Z_C and V_s. Therefore,
    I_{x_2}=\frac{V_s}{R+Z_C}
    =\frac{2}{1-j0.5}
    =\frac{2\times (1+j0.5)}{(1-j0.5)\times (1+j0.5)}
    =\frac{2+j}{1^2+0.5^2}
    =\frac{2+j}{1.25}
    =1.6+j0.8
    =1.789\angle 26.6^{\circ}

    Time domain

    i_{x_2}(t)=1.789 \sin (2t+26.6^{\circ}) ~ \text{A}
    (why \sin?)

    Answer

    Now that we have determined both i_{x_1}(t) and i_{x_2}(t) in time domain, we can go ahead and add them up to find i_x(t). Please note that we could not add I_{x_1} and I_{x_2} because they are not phasors with the same frequency.
    i_{x}(t)=i_{x_1}(t)+i_{x_2}(t)=0.97 \cos (4t-76^{\circ}) + 1.789 \sin (2t+26.6^{\circ}) ~ \text{A}
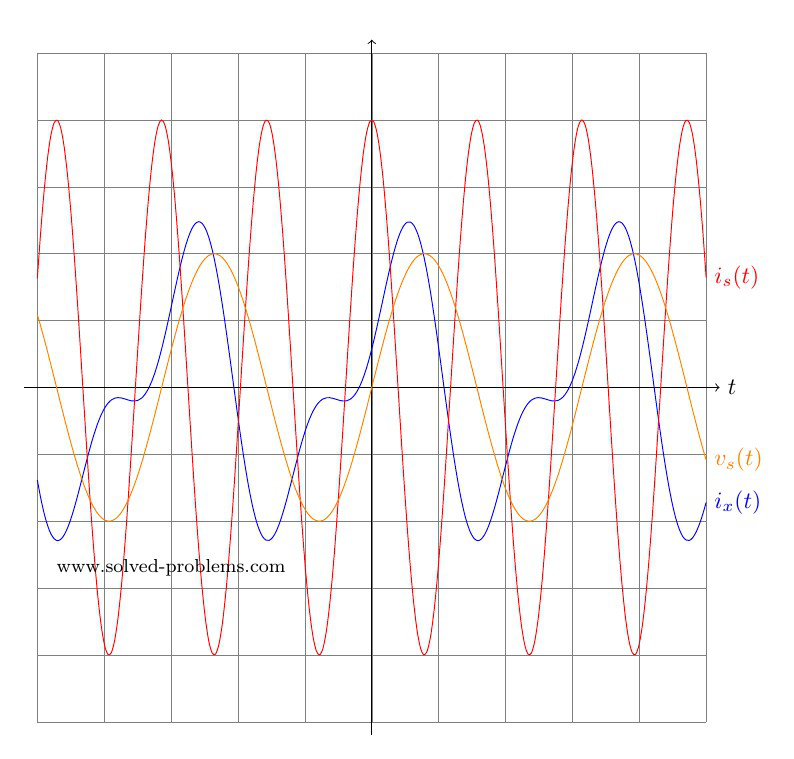
    signal plots - AC Circuit Analysis with superposition theorem

  • Mesh (Current) Analysis Problem

    Mesh (Current) Analysis Problem

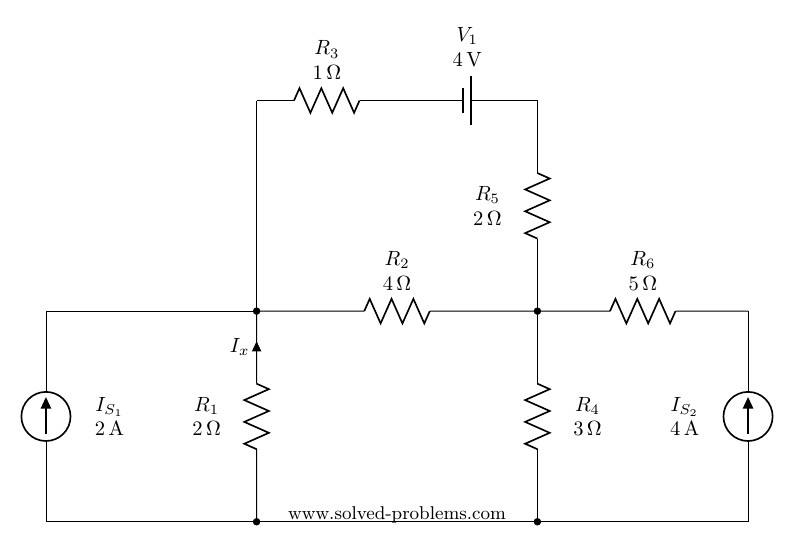
    Solve the circuit by mesh analysis and find the current I_x and the voltage across R_2.
    mesh analysis problem

    Solution

    Mesh Analysis

    There are four meshes in the circuit. So, we need to assign four mesh currents. It is better to have all the mesh currents loop in the same direction (usually clockwise) to prevent errors when writing out the equations.
    (more…)

  • Stability using Routh Stability Criterion

    Stability using Routh Stability Criterion

    Determine the stability of the system whose characteristics equation is:

    a(s) = 2s^5 + 3s^4 + 2s^3 + s^2 + 2s + 2.

    Solution

    All coefficients are positive and non-zero; therefore, the necessary condition for stability is satisfied. Let’s write the Routh array:

    \begin{array}{l | c c c} s^5 & 2 & 2 & 2 \\ s^4 & 3 & 1 & 2 \\ s^3 & & & \\ s^2 & & & \\ s^1 & & & \\ s^0 & & &\end{array}
    (more…)

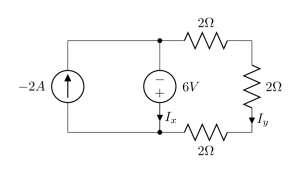
  • Winner of Electrical Circuits Contest #1

    Winner of Electrical Circuits Contest #1

    Problem

    Find I_x and I_y :
    Electrical Circuit Contest #1

    Solution

    Three resistors are in series and their equivalent, 6\Omega, is parallel with the voltage source. So, according to the Ohm’s law: I_y=-\frac{6V}{6 \Omega}=-1 A. The negative sign comes from the direction I_y.
    Applying KCL at the bottom node:
    -(-2A)+I_x+I_y=0 \rightarrow I_x=-1 A.
    The lucky winner of the Electrical Circuits Contest #1 is Kunal Marwaha from UC Berkeley. I would like to say thank you to all participants and I am thinking of holding contest #2 soon. Kunal, congratulations and soon you will receive the prize by Paypal.

  • Find Equivalent Impedance – AC Steady State Analysis

    Determine the driving-point impedance of the network at a frequency of 2kHz:

    Determine Impedance

    Solution

    Lets first find impedance of elements one by one:

    Resistor R

    The resistor impedance is purely real and independent of frequency.

    Z_R=R=20 \Omega

    (more…)