Solved Problems

Stability using Routh Stability Criterion

Written by

Yaz

in

,

Determine the stability of the system whose characteristics equation is:

a(s) = 2s^5 + 3s^4 + 2s^3 + s^2 + 2s + 2.

Solution

All coefficients are positive and non-zero; therefore, the necessary condition for stability is satisfied. Let’s write the Routh array:

\begin{array}{l | c c c} s^5 & 2 & 2 & 2 \\ s^4 & 3 & 1 & 2 \\ s^3 & & & \\ s^2 & & & \\ s^1 & & & \\ s^0 & & &\end{array}

At this stage, we see that the top row corresponding to S^5 can be divided by two to make the calculation a little bit easier. So, we go ahead and divide that row by two:

\begin{array}{l | c c c} s^5 &1 & 1 & 1 \\ s^4 &3 & 1 & 2 \\ s^3 &\\ s^2 &\\s^1 &\\s^0\end{array}

Let’s continue writing the Routh table:

\begin{array}{l | c c c}s^5 &1 & 1 & 1 \\ s^4 &3 & 1 & 2 \\ s^3 &\frac{3 \times 1 - 1 \times 1}{3}&\frac{3 \times 1 - 2 \times 1}{3} & \\ s^2 &\\s^1 &\\s^0 \end{array}

\begin{array}{l | c c c}s^5 &1 & 1 & 1 \\ s^4 &3 & 1 & 2 \\ s^3 & \frac{2}{3} & \frac{1}{3} & \\ s^2 & \frac{\frac{2}{3} \times 1 - \frac{1}{3} \times 3}{\frac{2}{3}} & \frac{\frac{2}{3} \times 2 - 0 \times 3}{\frac{2}{3}} & \\s^1 & \\s^0 &\end{array}

\begin{array}{l | c c c}s^5 &1 & 1 & 1 \\ s^4 &3 & 1 & 2 \\ s^3 &\frac{2}{3} &\frac{1}{3} & \\ s^2 &-\frac{1}{2} & 2 & \\s^1 &\frac{-\frac{1}{2} \times \frac{1}{3} - 2 \times \frac{2}{3}}{-\frac{1}{2}} &\\s^0 \end{array}

\begin{array}{l | c c c}s^5 &1 & 1 & 1 \\ s^4 &3 & 1 & 2 \\ s^3 &\frac{2}{3} &\frac{1}{3} & \\ s^2 &-\frac{1}{2} & 2 & \\s^1 &3 & \\s^0 & \frac{3 \times 2 -0 \times -\frac{1}{2}}{-\frac{1}{2}}\end{array}

\begin{array}{l | c c c}s^5 &1 & 1 & 1 \\ s^4 & 3 & 1 & 2 \\ s^3 &\frac{2}{3} &\frac{1}{3} & \\ s^2 &-\frac{1}{2} & 2 & \\s^1 &3 & \\s^0 & 2 \end{array}

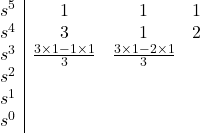
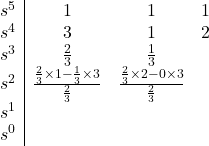
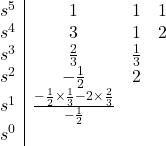
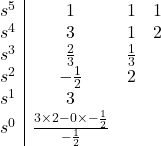
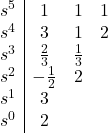
Since there are two sign changes in the first column, the characteristic equation has two roots with negative real parts. Therefore, the system is unstable.

Comments

One response to “Stability using Routh Stability Criterion”

  1. muhsin alam Avatar
    muhsin alam

    plz provide solution manual of electric circuit fundamental by sergio franco

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

More posts