Problem 2-10: Diffrentiating

Diffrentiate
a) $f_1\left(x\right)= \displaystyle\frac{1-2x^2}{1+x+x^2}$
b) $f_2\left(x\right)= (1-2x^2)(1+x+x^2)$

Solution
The following rules can be used:
I) $\displaystyle\frac{d}{dx}ax^n=anx^{n-1}$
II) $\displaystyle\frac{d}{dx}\left(u+v\right)=\frac{du}{dx}+\frac{dv}{dx}$

III) $\displaystyle\frac{d}{dx}\left(uv\right)=u\frac{dv}{dx}+v\frac{du}{dx}$
IV) $\displaystyle\frac{d}{dx}\frac{u}{v}=\frac{1}{v^2}\left(v\frac{du}{dx}-u\frac{dv}{dx}\right)$

In both cases, set
$u=1-2x^2$ and $v=1+x+x^2$ . Using rules I and II:
$\frac{du}{dx}=0-2\times 2 x^{2-1}=-4x$

$\frac{dv}{dx}=0+1\times x^{1-1}+2x^{2-1}=1+2x$

a) $f_1\left(x\right)= \displaystyle\frac{1-2x^2}{1+x+x^2}=\frac{u}{v}$
According to rule IV,
$\displaystyle\frac{d}{dx}f_1(x)=\frac{1}{v^2}\left(v\frac{du}{dx}-u\frac{dv}{dx}\right)$
$\displaystyle\frac{1}{(1+x+x^2)^2}\left((1+x+x^2)(-4x)-(1-2x^2) (1+2x)\right)$
$=\displaystyle\frac{1}{(1+x+x^2)^2}\left(-4x-4x^2-4x^3-1-2x+2x^2 +4x^3)\right)$
$=\displaystyle\frac{-1-6x-2x^2}{(1+x+x^2)^2}$ .
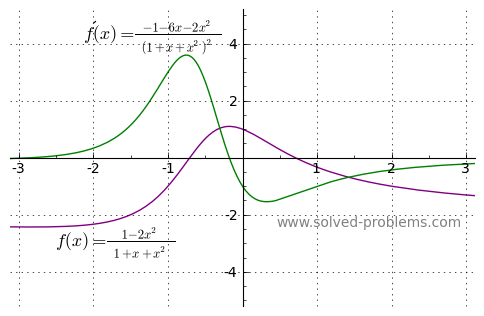
Problem 2-10-a

b) $f_2\left(x\right)= (1-2x^2)(1+x+x^2)=uv$
According to rule III,
$\displaystyle\frac{d}{dx}f_2(x)=u\frac{dv}{dx}+v\frac{du}{dx}=(1-2x^2)(1+2x)+(1+x+x^2)(-4x)$
$=1+2x-2x^2-4x^3-4x-4x^2-4x^3= 1-2x-6x^2-8x^3$ .
Problem 2-10-b

Problem 2-10: Diffrentiating

Published by Yaz

Leave a comment

Cancel reply