Solved Problems

Author: Yaz

  • Thévenin’s Theorem – Circuit with An Independent Source

    Thévenin’s Theorem – Circuit with An Independent Source

    Use Thévenin’s theorem to determine V_O .

    A circuit with a voltage source
    Fig. (1-26-1) – The Circuit

    Solution
    To find the Thévenin equivalent, we break the circuit at the 4\Omega load as shown below.
    (more…)

  • Superposition Method – Circuit With Dependent Sources

    Superposition Method – Circuit With Dependent Sources

    Determine I_x , I_y and V_z using the superposition method.

    Superposition - Circuit with dependent sources

    Solution
    I. Contribution of the -2V voltage source:
    We need to turn off the current source by replacing it with an open circuit. Recall that we do not turn off dependent sources. The resulting circuit is shown below.
    (more…)

  • Superposition Problem with Four Voltage and Current Sources

    Superposition Problem with Four Voltage and Current Sources

    Determine V_x and I_x using the superposition method.
    A circuit with four voltage and current sources to be solved by the superposition method
    Solution
    I. Contribution of the -5V voltage source:

    To find the contribution of the -5V voltage source, other three sources should be turned off. The 3V voltage source should be replaced by short circuit. The current source should be replaced with open circuits, as shown below.
    (more…)

  • Turning Sources Off

    Turning Sources Off

    Turning off a source, which is usually used in solving circuits with superposition method, means setting its value equal to zero. For a voltage source, setting the voltage equal to zero means that it produces zero voltage between its terminals. Therefore, the voltage source must insure that the voltage across two terminals is zero. Replacing the source with a short circuit can do that. Thus, voltage sources become a short circuit when turned off.

    For a current source, setting the current equal to zero means that it produces zero current. Therefore, the current source must insure that no current flows through its branch. An open circuit can do that. Hence, to turn off a current source it should be replaced by an open circuit.

    How about dependent sources? The voltage/current of a dependent source is dependent on other variables of the circuit. Therefore, dependent sources cannot be turned off.

    Example I: Turn off sources one by one.

    turning sources off example 1-1
    Example 1

    Solution:
    I) The voltage source:

    turning sources off example 1-2
    Turning off the voltage source

    (more…)

  • Solving Quadratic Equations II: Taking Square Roots

    A quadratic equation can be solved by taking the square root of both sides of the equation. This method uses the square root property,
    y^2=z \to y=\pm \sqrt{z}
    Before taking the square root, the equation must be arranged with the x2 term isolated on the left- hand side of the equation and its coefficient reduced to 1. There are four steps in solving quadratic equations by this method:
    (more…)

  • Solving Quadratic Equations I: Factoring (Grouping)

    Sometimes, quadratic equations can be solved by factorizing, which is also called grouping. The solve by factoring process is usually consists of three major steps:
    All terms should be moved to one side of the equation using addition or subtraction. Rewrite the equation so that the left side of the equation is set equal to 0. For example, if the original equation is x^2 = 5x - 3, it should be rewritten as x^2 - 5x + 3 = 0 .
    The equation should be factored completely. It will have two factors.
    Each factor should be set equal to zero. Since factors are of first power, they are easy to be solved.
    All of the solutions should be combined to obtain the full solution set for the original equation.
    The catch of this method is the finding of factors. Except some trivial cases, factoring quadratic equations is not easier than using other methods to solve the quadratic equations. Here are a few tips to help you factorize a quadratic equations:

    (more…)

  • Solving Equations II: Radical Equations

    A radical equation is an equation in which a variable appears under a radical sign. It may also have more than one radical. Let’s see some examples of radical equations:

    \sqrt{x-1}=2

    \sqrt{2x+4}=\sqrt{5}

    \sqrt{4x+1}+2x=-1

    \sqrt{x+1}=\sqrt{2x+1}+10

    \sqrt{10-x}+\sqrt{x-5}=3

    \sqrt{x^2+3}=3

    \sqrt[3]{2x-4}=-4

    \sqrt{\sqrt{x+2}+7}=4

    \sqrt[3]{x^2-1}=1

    \sqrt[3]{6x^2+2}-1=x

    (more…)

  • Solving Equations I: Linear Equations

    In a linear equation, each term is either a constant or the product of a constant and a single variable of degree 1. It can have one or more variables. Here are some linear equations:

    x+1=0
    2x+4=6
    -3x+1=x+4
    1+5x=0
    2-3x=3+2x
    \frac{1}{2}x+\frac{3}{4}=\frac{1}{3}
    \frac{x-1}{3}+\frac{1}{4}=\frac{5}{2}
    \frac{x}{c}+b=a where c\neq 0 is a constant
    \sqrt{3}x-\sqrt{2}=\sqrt{5}

    However, the following equations are not linear:
    (more…)

  • Nodal Analysis

    Screenshots

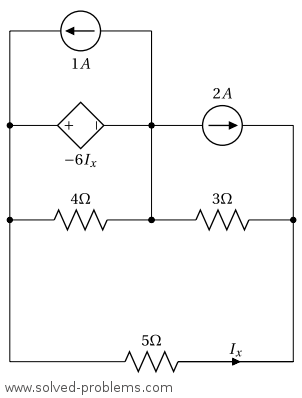
  • Nodal Analysis – Dependent Voltage Source (5-Nodes)

    Nodal Analysis – Dependent Voltage Source (5-Nodes)


    Solve the circuit with the nodal analysis and determine I_x.


    Nodal analysis - circuit with dependent voltage source


    Solution
    1) Identify all nodes in the circuit. Call the number of nodes N.
    There are five nodes in the circuit:

    (more…)