Solved Problems

Author: Yaz

  • Nodal Analysis – Super-node: a Non-grounded Voltage Source

    Nodal Analysis – Super-node: a Non-grounded Voltage Source

    Use nodal analysis to solve the circuit and determine the values of I_x and V_y.

    I. Identify all nodes in the circuit.
    There are four nodes in the circuit:

    (more…)
  • Nodal Analysis Problem with Dependent Voltage and Current Sources

    Nodal Analysis Problem with Dependent Voltage and Current Sources

    Solve the circuit with the nodal analysis and determine i_x and V_y.
    nodal analysis problem with dependent voltage and current sources

    Solution
    1) Identify all nodes in the circuit. Call the number of nodes N.
    The circuit has 5 nodes. Therefore, N=5.
    (more…)

  • Reference Node and Node Voltages

    Reference Node
    In circuits, we usually label a node as the reference node also called ground and define the other node voltages with respect to this point. The reference node has a potential of 0 V by definition. The following symbol is used to indicate the reference node:

    The Reference Node Symbol
    The Reference Node Symbol

    As mentioned, the selection of the reference node is arbitrary. However, a wise selection can make the solving easier. As a general rule, it is usually chosen to be
    (more…)

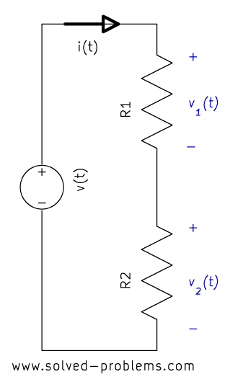
  • Voltage Divider – Voltage Division Rule

    Voltage Divider – Voltage Division Rule

    The voltage division rule (voltage divider) is a simple rule which can be used in solving circuits to simplify the solution. Applying the voltage division rule can also solve simple circuits thoroughly. The statement of the rule is simple:

    Voltage Division Rule: The voltage is divided between two series resistors in direct proportion to their resistance.

    It is easy to prove this. In the following circuit

    Voltage Divider
    Voltage Divider

    the Ohm’s law implies that
    v_1(t)=R_1 i(t) (I)
    v_2(t)=R_2 i(t) (II)
    (more…)

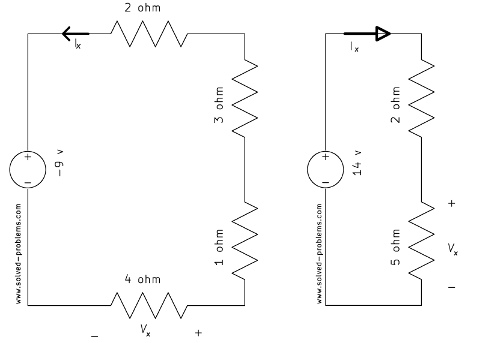
  • Problem 1-16: Voltage Divider

    Problem 1-16: Voltage Divider

    Find V_x (or v_x(t)) and I_x (or i_x) using voltage division rule.
    a)
    Voltage Divider Problem - A
    b)
    Voltage Divider Problem - B
    c)
    Voltage Divider Problem - C
    d)
    Voltage Divider Problem - D

    Solution

    a)
    Voltage Divider Problem - A
    Voltage divider: V_x=\frac{5\Omega}{2\Omega+5\Omega}\times 14 V=10 V
    Ohm’s law: I_x=\frac{V_x}{5 \Omega}=2 A
    (more…)

  • Ideal Independent Sources

    Ideal Independent Sources

    1) Ideal Independent Voltage Sources
    An ideal independent voltage source is a two-terminal circuit element where the voltage across it
    a) is independent of the current through it
    b) can be specified independently of any other variable in a circuit.
    There are two symbols for ideal independent voltage source in circuit theory:

    Symbol for Constant Independent Voltage Source
    Symbol for Constant Independent Voltage Source

    (more…)

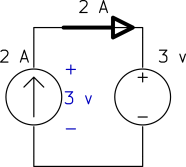
  • Problem 1-15: Power of Independent Sources

    Problem 1-15: Power of Independent Sources

    Determine the power of each source.
    a)
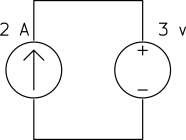
    Voltage and Current Sources
    b)
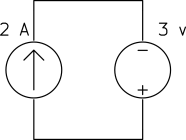
    Voltage and Current Sources

    Solution
    a) The current source keeps the current of the loop 2A and the voltage source keeps the voltage across the current source 3v as shown below.
    (more…)

  • Problem 1-14: Current of A Voltage Source

    Problem 1-14: Current of A Voltage Source

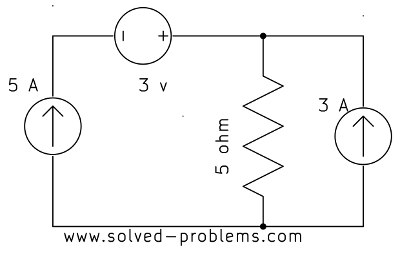
    Find the current passing through the voltage source:
    a)
    A voltage source in series with a current source
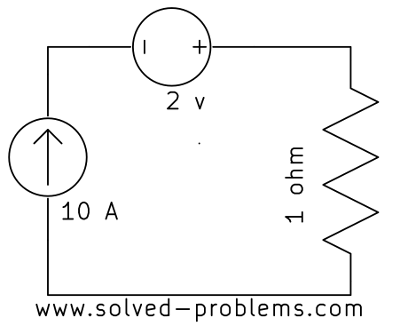
    b)
    A voltage source in series with a current source and other elements

    Solution
    a) The voltage source is in series with the current source. Since by definition a current source keeps the current passing through itself constant and the voltage source is in series with the current source, it should have the same current 10 A.
    (more…)

  • Problem 1-13: Voltage of A Current Source

    Problem 1-13: Voltage of A Current Source

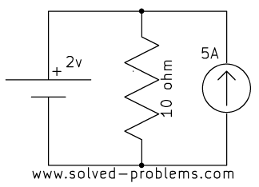
    Find voltages across the current sources.
    a)
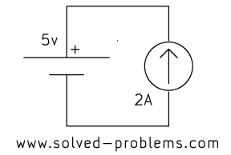
    A Current Source Parallel with A Voltage Source
    b)
    Voltage Across Parallel Elements
    c)
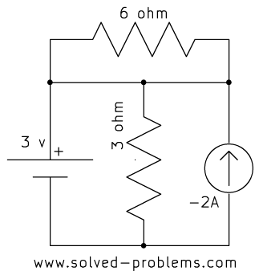
    Parallel Current and Voltage Sources
    d)
    Parallel Current and Voltage Sources
    e)
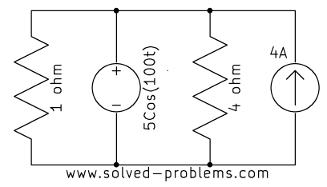
    Parallel Current and Variable Voltage Sources

    Solution

    In each case, the current source is parallel with a voltage source. Therefore, the voltage across the current source is equal to the voltage of the voltage source, regardless of other elements.
    (more…)

  • Problem 1-12: Using Voltage Sources to Determine Node Voltages

    Problem 1-12: Using Voltage Sources to Determine Node Voltages

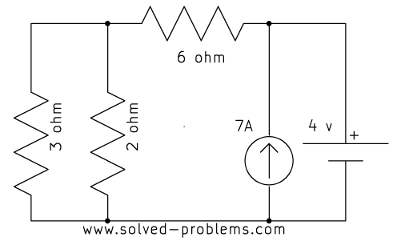
    Determine the power of R_1, R_2 and Vs_1. (Hint: there is no need to use nodal analysis; voltages between nodes can be easily found by the voltage sources.)
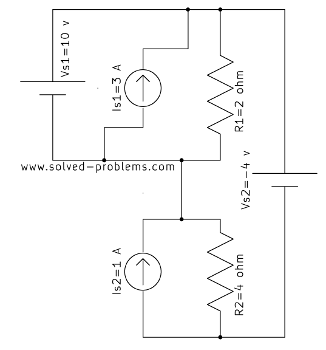
    Voltage sources can be used to fing node voltages

    Solution
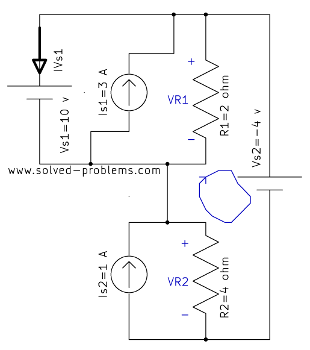
    KVL around the loop
    V_{R_1}= Vs_1 = 10v \rightarrow P_{R_1}=\frac{V_{R_1}^2}{R_1}=50 W
    (more…)