Determine the stability of the system whose characteristics equation is:
![]() .
.
Solution
All coefficients are positive and non-zero; therefore, the necessary condition for stability is satisfied. Let’s write the Routh array:

At this stage, we see that the top row corresponding to ![]() can be divided by two to make the calculation a little bit easier. So, we go ahead and divide that row by two:
can be divided by two to make the calculation a little bit easier. So, we go ahead and divide that row by two:

Let’s continue writing the Routh table:
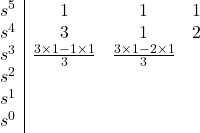
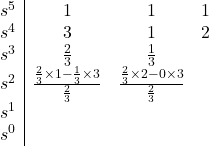
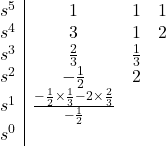
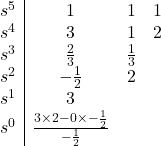
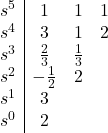
Since there are two sign changes in the first column, the characteristic equation has two roots with negative real parts. Therefore, the system is unstable.
Leave a Reply