Nodal Analysis – Dependent Voltage Source (5-Nodes)

Solve the circuit with the nodal analysis and determine .


Solution
1) Identify all nodes in the circuit. Call the number of nodes .
There are five nodes in the circuit:


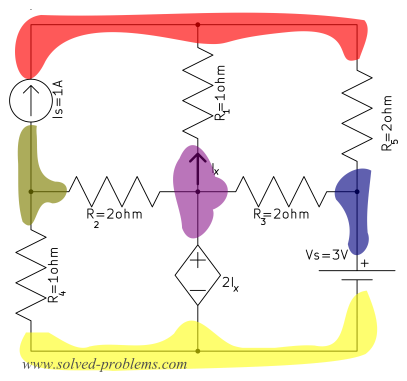
Therefore
2) Select a reference node
The best option is the node in the bottom because it is connected to both voltage sources.


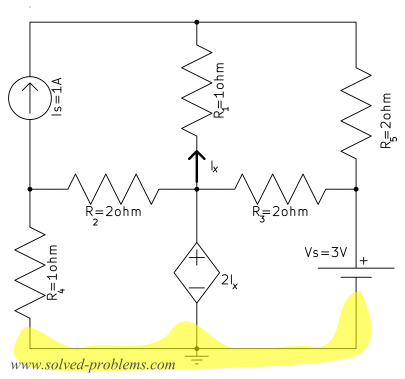
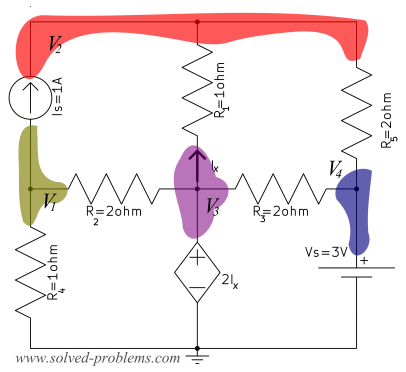
3) Assign a variable for each node whose voltage is unknown.
There are four nodes beside the reference node:


Node III and Node IV are connected to the reference node through voltage sources. Therefore, their node voltages can be determined by the voltage sources.
and .

is the current of . The Ohm’s law can be used to write in terms of the node voltages. Thus, . Substituting , (Eq. 1).
Therefore, .
4) Write down KCL equations.
We only need to write a KCL equation for Node I and Node II:
Node I: . Substituting and known variables,
(Eq. 2).

Node II: . .
Substituting in Eq. 2:
.

Now, we need to determine the required quantities. Eq. 1 implies that
.