Solved Problems

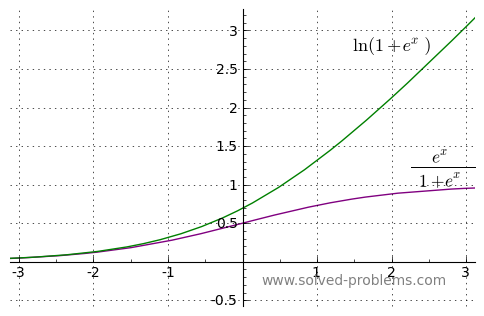
Problem 2-8: Integration

Written by

Yaz

in

,

Find \displaystyle\int \! \frac{e^x}{1+e^x}\, dx.

Solution

Let u=1+e^x, therefore du=e^x dx \to dx=\frac{1}{u-1}du. Hence

\displaystyle\int \! \frac{e^x}{1+e^x}\, dx = \displaystyle\int \! \frac{u-1}{u} \frac{1}{u-1}\,du = \displaystyle\int \! \frac{1}{u} \,du=\ln (u)=\ln(1+e^x)
Problem 2-8

Master Nodal Analysis with ease!

I’ll send you a simple yet powerful guide to help you tackle circuit problems effortlessly.

​

Get the free eBook by subscribing below.

    We respect your privacy. Unsubscribe at any time.
    Built with Kit

    Comments

    3 responses to “Problem 2-8: Integration”

    1. jose flaminio tellez abril Avatar
      jose flaminio tellez abril

      aprender a integrar


      _____________
      learned to integrate

      Reply
    2. yohannes berhanu Avatar
      yohannes berhanu

      i really appreciate if u can send me newsletter every week. i am a pre college student , and i am glad to have this kind of website that would enable me and other fellas to succed on their academic activities.

      Reply
      1. Dr. Yaz Z. Li Avatar
        Dr. Yaz Z. Li

        Dear Yohannes,

        I am thinking of starting a newsletter. All registered user would be receiving it.

        Reply

    Leave a Reply

    Your email address will not be published. Required fields are marked *

    More posts