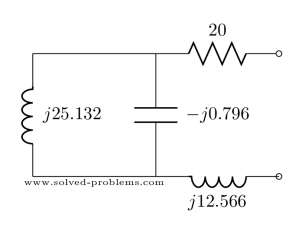
Determine the driving-point impedance of the network at a frequency of ![]() kHz:
kHz:
Solution
Lets first find impedance of elements one by one:
Resistor 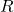
The resistor impedance is purely real and independent of frequency.
![]()
Inductors 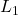 and
and 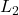
The inductor impedance is purely imaginary and directly proportional to frequency:
![]()
We need to find the impedance in ![]() kHz. Therefore:
kHz. Therefore:
![]()
![]()
![]()
Capacitor 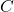
The capacitor impedance is purely imaginary and inversely proportional to frequency:
![]()
To get the standard representation of complex numbers, we need to bring ![]() to numerator and this can be done by multiplying by
to numerator and this can be done by multiplying by ![]() :
:
![]()
Note how capacitor acts in this frequency. The value of impedance is less than ![]() . Compare this value to values of other components. It is almost equivalent to a short circuit!
. Compare this value to values of other components. It is almost equivalent to a short circuit!
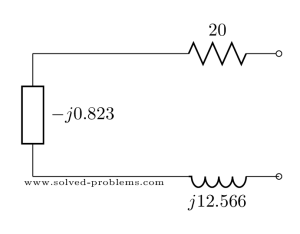
Equivalent Impedance
Let’s replace the values in the circuit:
![]() and
and ![]() are parallel.
are parallel.
![]()
One interesting point here is that unlike pure resistive circuits where the equivalent resistance of parallel elements is always less than the resistance of each element, the value of the equivalent impedance of parallel elements can be greater than the value of the impedance of elements. Here the capacitor impedance value is ![]() but the equivalent impedance,
but the equivalent impedance, ![]() , is higher.
, is higher.
Three components are in series. Therefore:
![]()
Now, determine the impedance at ![]() Hz and
Hz and ![]() kHz and share it with others below in comments section.
kHz and share it with others below in comments section.

Leave a Reply to Yaz Cancel reply