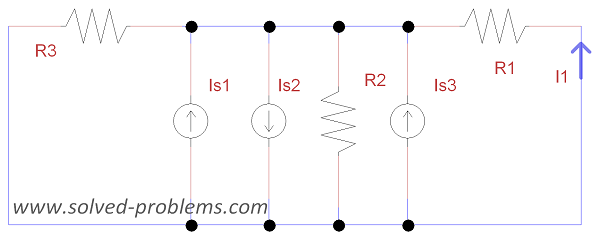
Find 
using single node-pair analysis (do not reduce the circuit).
and 
.
Solution
a) Redraw the circuit if necessary. Mark the voltage across nodes:
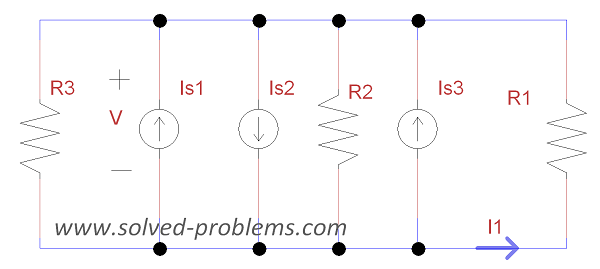
b) Apply KCL in one of nodes:
.
Please note that:
i) Voltage across each element is 
with the shown polarity.
ii) We do not use , because it is unknown. We try to find any current in term of the main quantity, i.e. , which is unknown. Recall that main quantities are
- node voltages in nodal analysis,
- node voltage in single-node-pair analysis,
- loop current in single loop analysis, and
- mesh currents in mesh analysis.
iii) Since we are not using , we do not care about its direction.
Eq. (1) gives 
.
c) Determine required quantity, using main quantity, i.e. :
