Find resistor currents using KVL.
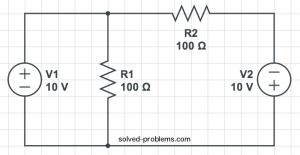
Solution:
![]() and
and ![]() are parallel. So the voltage across
are parallel. So the voltage across ![]() is equal to
is equal to ![]() . This can be also calculated using KVL in the left hand side loop:
. This can be also calculated using KVL in the left hand side loop:
![]() .
.
Now, use Ohm’s law to find ![]() :
:
![]() .
.
To find ![]() , write KVL around the outer loop:
, write KVL around the outer loop:
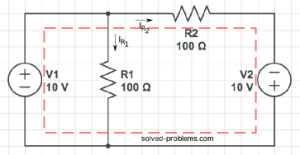
![]() .
.
Again, use Ohm’s law to determine ![]() :
:
![]() .
.
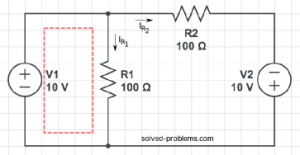
Now, tell me what is the current passing through ![]() ?
?

Leave a Reply