Voltage Divider – Voltage Division Rule

Written by

Electrical Circuits, Electrical Circuits Articles

The voltage division rule (voltage divider) is a simple rule which can be used in solving circuits to simplify the solution. Applying the voltage division rule can also solve simple circuits thoroughly. The statement of the rule is simple:

Voltage Division Rule: The voltage is divided between two series resistors in direct proportion to their resistance.

It is easy to prove this. In the following circuit

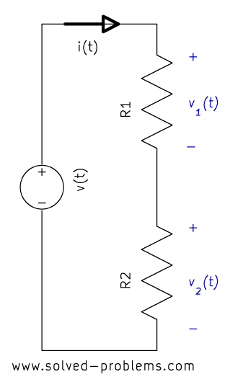
Voltage Divider

the Ohm’s law implies that
$v_1(t)=R_1 i(t)$ (I)
$v_2(t)=R_2 i(t)$ (II)

Applying KVL
$-v(t)+v_1(t)+v_2(t)=0 \rightarrow v(t)=v_1(t)+v_2(t)$ .

Therefore
$v(t) = R_1 i(t)+R_2 i(t)= (R_1 +R_2) i(t)$ .

Hence
$i(t) = \frac{v(t)}{R_1 +R_2}$ .

Substituting in I and II
$v_1(t)=R_1 \frac{v(t)}{R_1 +R_2}$ ,
$v_2(t)=R_2 \frac{v(t)}{R_1 +R_2}$ .

Consequently

$v_1(t)= \frac{R_1}{R_1 +R_2} v(t)$ ,
$v_2(t)=\frac{R_2}{R_1 +R_2} v(t)$ .

which shows that the voltage is divided between two series resistors in direct proportion to their resistance. The rule can be easily extended to circuits with more than two resistors. For example,

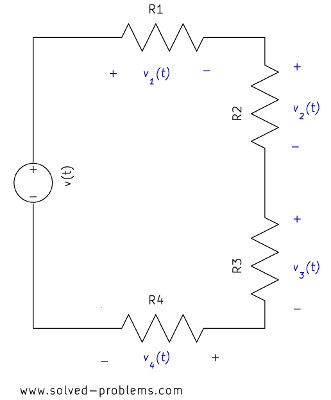
Voltage Division among four resistors

$v_1(t)= \frac{R_1}{R_1 +R_2+R_3+R_4} v(t)$ ,
$v_2(t)=\frac{R_2}{R_1 +R_2+R_3+R_4} v(t)$ ,
$v_3(t)=\frac{R_3}{R_1 +R_2+R_3+R_4} v(t)$ ,
$v_4(t)=\frac{R_4}{R_1 +R_2+R_3+R_4} v(t)$ .

The voltage division rule can be used solve simple circuits or to simplify solving complicated circuits.
For example, check out this problem.

One of the common mistakes in using the voltage division rule is to use the formula for resistors which are in parallel with other elements. For example, the voltage division rule cannot be used in the following circuit directly.
voltage divider - misleading case - a

It will be incorrect if one tries to find $V_x$ using voltage divider by neglecting the other $6 \Omega$ resistor as
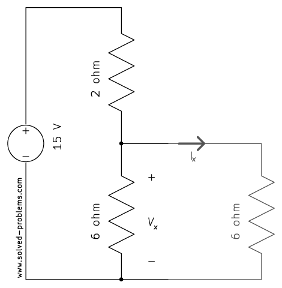
voltage divider - misleading case - b

So, $V_x \neq \frac{6 \Omega}{2 \Omega + 6 \Omega} 15 V$ . However, if solving other parts of a circuits confirms that the current of the other element/branch is zero, the voltage division rule can be still applied. For example, suppose that the following network is a piece of a larger circuit.
voltage divider - piece of a larger circuit
Let’s assume that the analysis of the circuit shows that $I_x=0$ . In this case, $V_x= \frac{6 \Omega}{2 \Omega + 6 \Omega} 12 V = 9 V$ regardless of where A and B are connected.

The voltage devision rule can be used to ease solving problems. For example, the voltage division rule is used in the following problem to find the Thévenin voltage:
Thévenin’s Theorem – Circuit with An Independent Source
.

Comments

17 responses to “Voltage Divider – Voltage Division Rule”

April 6, 2011

malikana nyambe s

a parallel plate capacitor has area=2 mm and plate separation distance, d=1 mm. find how much charge is stored when the capacitor si connected to a 10 volts battery.

Reply
1. April 24, 2011
  
  Fox
  
  C = epsilonr*epsilon0*A/d
  Q=C*V
  
  Work it out for yourself!
  
  Reply
2. April 13, 2015
  
  Wiezzie
  
  The charge is 1.77e-16 coulombs
  
  Reply
September 13, 2011

Josh

Really usefull.Especially the voltage divider thing, I struggle with it in Polytechnic and Iam still struggling with it but thanks, I have cleared the confusion after going through your information.

Reply
March 2, 2012

sidd

really sooorry for last one. That is my younger brother’s deeds.valuable information. but you didnt mention any thing about parallel circuits.

Reply
March 26, 2012

Anand

Super

Reply
June 13, 2012

Sunil kumar.T

The voltage divider formulas and the solved problems are very useful to me. I corrected several circuits in our company. Thanks a lot for the support.

Reply
September 1, 2013

Tei

This is very helpful and easy to follow I can now complete my assignment

Reply
September 4, 2013

Rajiv

Thank uu so much

Reply
July 29, 2014

ALBERTO CHERU

the questions are very challenging and concept oriented…hence keep it up!!!

Reply
July 29, 2014

David

Confused about the line ‘now substitute in I and II’ what exactly is substituted? I cannot see where this step came from.

Reply
March 19, 2015

Singh

THANKS…USEFUL INFO…

Reply
October 1, 2015

Robert Sumner

Hi Yaz,

You seem to have a good page, but the graphics have either fallen away over time or otherwise are not present.

Thanks for the math, though — it was useful review and simplified expression!

Reply
June 18, 2018

A copper wire and an iron wire – Potential difference | Physics Forums

[…] got it. It has to do with the Kirchhoff's Voltage Law. Here is a website explaining it: http://www.solved-problems.com/circuits/circuits-articles/482/voltage-divider-voltage-division-rule/ Though I do find it odd that such an exercise comes before KVL is even introduced. […]

Reply
November 11, 2018

Ndatshi

A big noisy THANK YOU

Reply
July 1, 2019

Ngasoh Greg

Hi
Good and simple to understand. hope to see simple calculation to solve complicated circuit which comprises voltage and current sources

Greg

Reply
September 9, 2020

Harshit Thakur

hey,
really confused about the part where parallel circuits are given and voltage division rule cannot be applied directly. Isn’t voltage supposed to be equal across parallel resistances?

Reply