In AC circuit analysis, if the circuit has sources operating at different frequencies, Superposition theorem can be used to solve the circuit. Please note that AC circuits are linear and that is why Superposition theorem is valid to solve them.

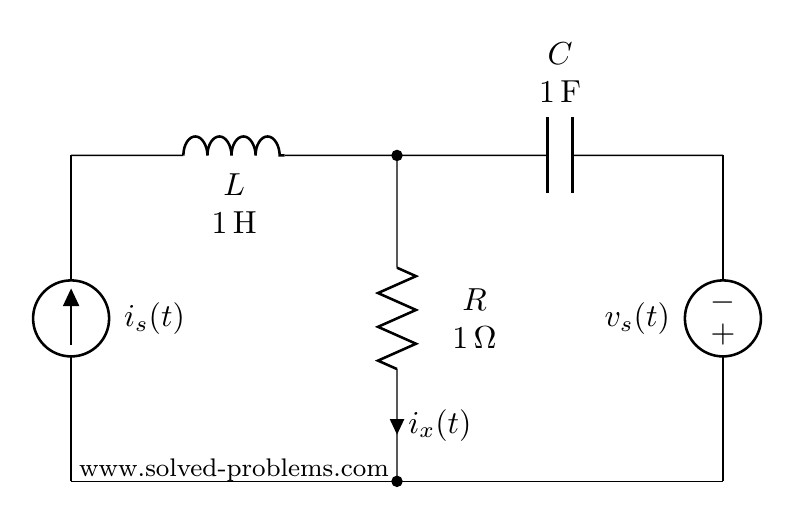
Problem

Determine i_x(t) where i_s(t)=4 \cos (4t) ~ A and v_s(t)=2 \sin (2t) ~ V.
ac circuit analysis with different source frequencies

Solution with AC Circuit Analysis

Since sources are operating at different frequencies, i.e. 4 \frac{rad}{s} and 2 \frac{rad}{s}, we have to use the Superposition theorem. That is to say that we need to determine contribution of each source on i_x(t). Then, the final answer is to obtained by adding the individual responses in the time domain. Please note that, since the impedances depend on frequency, we need to have a different frequency-domain circuit for each frequency.

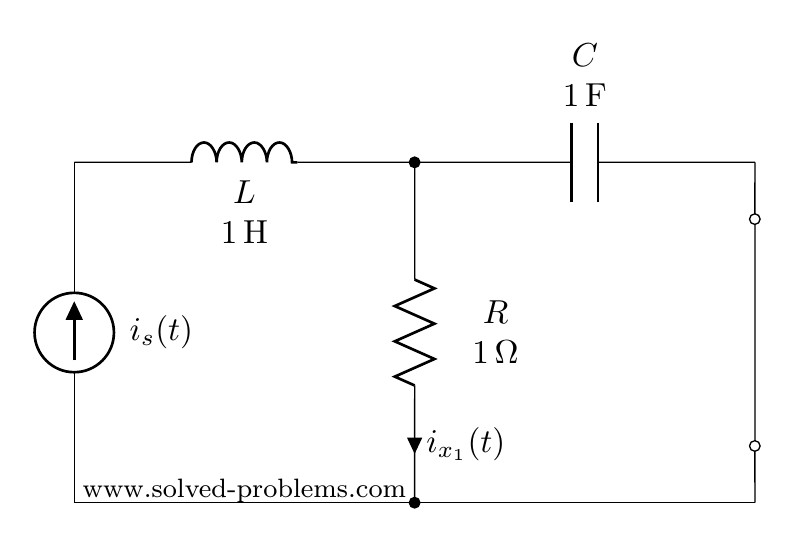
Contribution of the current source

To find the contribution of the current source, we need to turn off other source(s). So, we need to turn off the voltage source. This is very similar to DC circuits that we discussed before:

Voltage sources become a short circuit when turned off.

Turning off the voltage source for AC steady state circuit problem containing sources with different frequencies

Frequency domain

We first convert the circuit to the frequency domain:
i_s(t)=4 \cos (4t) ~ A \rightarrow I_s=4\angle 0^{\circ} (\omega = 4 \frac{rad}{s})
L=1\text{H} \rightarrow Z_L=j \omega L=j4
C=1\text{F} \rightarrow Z_C=\frac{1}{j \omega C}=\frac{1}{j4}=-j0.25
R=1 \Omega \rightarrow Z_R=R=1
i_{x_1}(t) \rightarrow I_{x_1}

Using current divider:
I_{x_1}=\frac{Z_C}{Z_C+R}I_s
=\frac{-j0.25}{-j0.25+1} \times 4
=\frac{-j0.25}{1-j0.25} \times 4
=\frac{-j0.25 \times (1+j0.25)}{(1-j0.25)\times (1+j0.25)} \times 4
=\frac{-j0.25 + 0.0625)}{1^2+0.25^2} \times 4
=\frac{-j0.25 + 0.0625)}{1.0625} \times 4
=0.235-j0.941
=0.97\angle -76^{\circ}

Time domain

Conversion to time-domain:
i_{x_1}(t)=0.97 \cos (4t-76^{\circ}) ~ \text{A}
Please note that the sinusoidal function for i_s(t) is cosine and consequently, cosine must be used in converting I_{x_1} to the time domain.

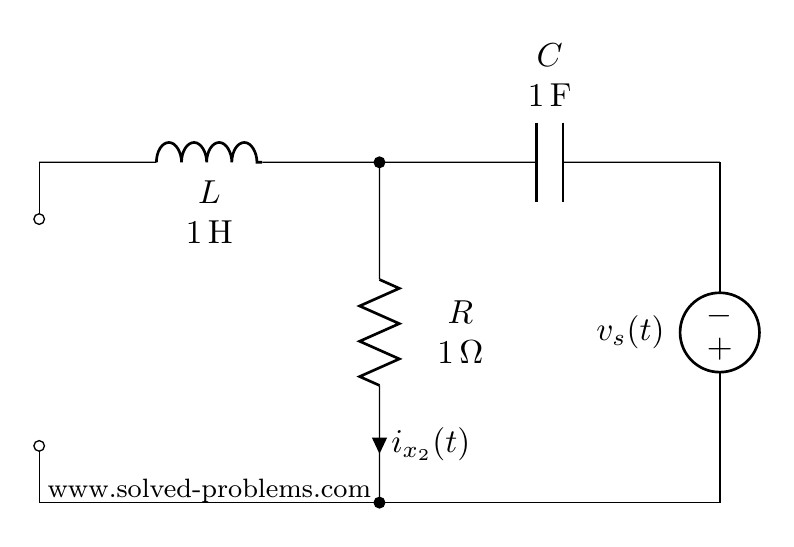
Contribution of the voltage source

To find the contribution of the voltage source, the current source needs to be turned off. As mentioned before:

To turn off a current source it should be replaced by an open circuit

Turning off the current source for AC steady state circuit problem containing sources with different frequencies

Frequency domain

v_s(t)=2 \sin (2t) ~ V \rightarrow V_s=2\angle 0^{\circ} (\omega = 2 \frac{rad}{s})
L=1\text{H} \rightarrow Z_L=j \omega L=j2
C=1\text{F} \rightarrow Z_C=\frac{1}{j \omega C}=\frac{1}{j2}=-j0.5
R=1 \Omega \rightarrow Z_R=R=1
i_{x_2}(t) \rightarrow I_{x_2}

As the inductor branch is open, this is a very simple circuit with three elements in series: R, Z_C and V_s. Therefore,
I_{x_2}=\frac{V_s}{R+Z_C}
=\frac{2}{1-j0.5}
=\frac{2\times (1+j0.5)}{(1-j0.5)\times (1+j0.5)}
=\frac{2+j}{1^2+0.5^2}
=\frac{2+j}{1.25}
=1.6+j0.8
=1.789\angle 26.6^{\circ}

Time domain

i_{x_2}(t)=1.789 \sin (2t+26.6^{\circ}) ~ \text{A}
(why \sin?)

Answer

Now that we have determined both i_{x_1}(t) and i_{x_2}(t) in time domain, we can go ahead and add them up to find i_x(t). Please note that we could not add I_{x_1} and I_{x_2} because they are not phasors with the same frequency.
i_{x}(t)=i_{x_1}(t)+i_{x_2}(t)=0.97 \cos (4t-76^{\circ}) + 1.789 \sin (2t+26.6^{\circ}) ~ \text{A}
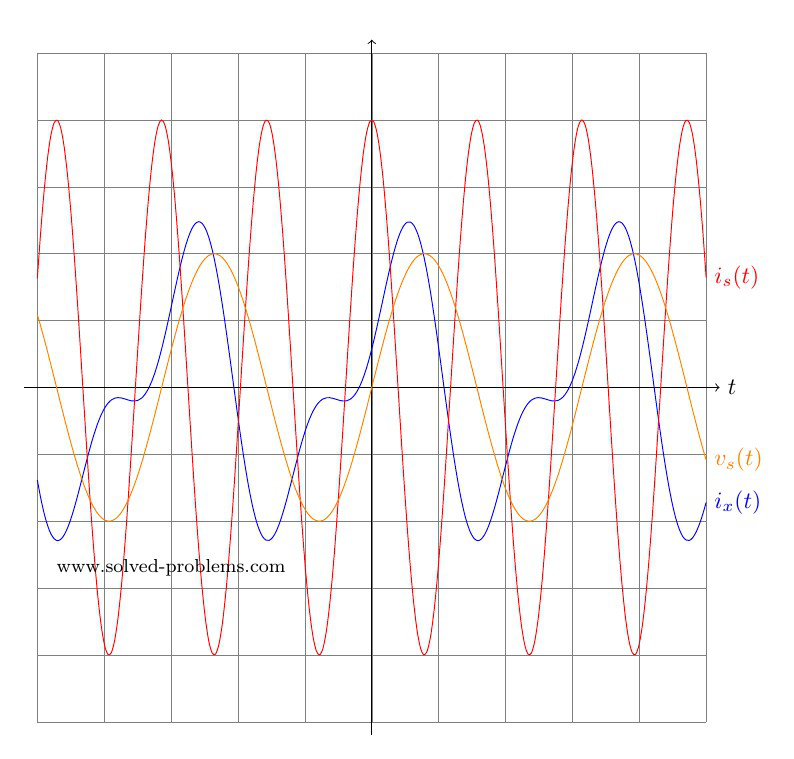
signal plots - AC Circuit Analysis with superposition theorem

Published by Yaz

Hi! Yaz is here. I am passionate about learning and teaching. I try to explain every detail simultaneously with examples to ensure that students will remember them later too.

Join the Conversation

3 Comments

  1. Reply
  2. Reply
  3. Reply

Leave a comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.