Find Thevenin’s and Norton’s Equivalent Circuits: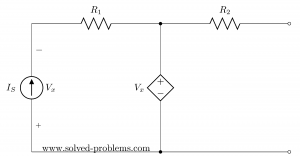

Suppose that $R_1=5\Omega$ , $R_2=3\Omega$ and $I_S=2 A$ .

Solution

The circuit has both independent and dependent sources. In these cases, we need to find open circuit voltage and short circuit current to determine Norton’s (and also Thevenin’s) equivalent circuits.

A PDF sheet of this problem with the solution and side space for notes can be downloaded below. Also, you may watch solving this problem on the video posted below. My suggestion is that you print the solution sheet and make notes on it while watching the video. Please subscribe to my YouTube channel for more videos!

Open circuit voltage

Open circuit voltage means the voltage across the terminals of the network without connecting any extra element or connection:

Since there is no connection, the current of $R_2$ is zero. To solve the circuit lets write KVL for the left hand side loop assuming $I_{R_1}$ defined from left to right:

$+V_x+R_1 \times I_{R_1}+V_x=0$
$\rightarrow 2V_x=-R_1 \times I_{R_1}$
$\rightarrow V_x=-\frac{R_1 \times I_{R_1}}{2}$
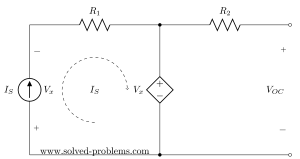
But what is $I_{R_1}$ ? $R_1$ is in series with the current source; they have only one node shared and there is no other element connected there. This means that all current of $I_{S}$ must pass through $R_1$ . Therefore, $I_{R_1}=I_{S}=2 A$ .
If we apply this to the equation above, we have

$V_x=-\frac{R_1 \times I_{R_1}}{2} \rightarrow V_x=-5 V$ .
Since no current passing through $R_2$ we can easily see that $V_{OC}=V_x$ . If it is not clear, you could find this by applying KVL to the right hand side loop:
$-V_x+R_2 \times I_{R_2}+V_{OC}=0$
$\rightarrow -V_x+R_2 \times 0+V_{OC}=0$
$\rightarrow V_{OC}=V_x=-5 V$

Short circuit current

Next, we need to find the short circuit current. It means we need to connect terminals of the network and calculate the current passing through the connection:

Doing so, we get a circuit with two loops. It is very important to note that all values might be changed and we are not allowed to use values/formulas of the open circuit voltage calculation. Just forget all and analyze the new circuit and calculate short circuit current $I_{SC}$ .

Please note that the mesh currents (loop currents for not-shared portion of loops) are as shown above. For the left hand side loop it is equal to the current of the current source as current sources enforce their current to go through all elements in series with them. For the right hand side loop it is $I_{SC}$ and there is no benefit in defining a new label for current.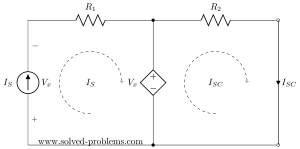

KVL for the left loop:
$+V_x+R_1 \times I_{R_1}+V_x=0$
Again, here the current of $I_{R_1}$ is equal to $I_{S}$ and $I_{R_1}=I_{S}=2 A$ .
$+V_x+5 \times 2+V_x=0$
$\rightarrow V_x=-5 V$ .
We get the same value for $V_x$ . This is not a general rule and value could be different.
For the right hand side loop:

$-V_x+R_2 \times I_{SC}=0$
$I_{SC}=\frac{V_x}{R_2}=-\frac{5}{3} A$

Thevenin’s and Norton’s Equivalent Networks

The only thing left is to calculate $R_{th}$ which can be easily found by
$R_{th}=\frac{V_{OC}}{I_{SC}}=\frac{-5}{-\frac{5}{3}}=3 \Omega$

Thevenin’s Equivalent Network

$V_{th}=V_{OC}=-5 V$
$R_{th}=3 \Omega$

Norton’s Equivalent Network

$I_{no}=I_{SC}=-\frac{5}{3} A$
$R_{no}=R_{th}=3 \Omega$

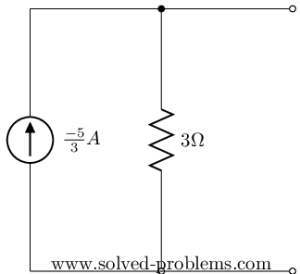
Now, assume that a [/latex]2 V[/latex] voltage source is connected to the terminals of this network, what would be its current?

Solution sheet

Find-Thevenins-and-Nortons-Equivalent-Circuits-Solved-Problems Download

Cancel reply

Join the Conversation

8 Comments

VIJAY says:

October 11, 2013 at 8:01 am

WHY INDEPENDENT SOURCE VALUSE COUNT TWOTIME IN KVL LAW

1. Yaz says:
  
  October 12, 2013 at 6:36 am
  
  A good question.
  It is not count two times. In KVL one of them is for the dependent voltage source and second one is for the voltage drop of the current source.
  Let me know if you need more explanations.
  
rajasekhar says:

March 8, 2014 at 5:28 pm

nice

Azhar says:

November 26, 2014 at 8:33 pm

Nice explanation

Danyal says:

January 24, 2015 at 7:16 am

How do we solve nortons with 2voltage source and 1 current source present in between two of them.! For Isc only.?

DANISH AKHTAQ says:

March 28, 2015 at 2:30 am

What is load resistance?

wesonga oliver says:

March 30, 2015 at 5:49 am

what if the dependent current source depends on the thevenin’s voltage

prashant pandey says:

August 8, 2015 at 11:51 am

excellent explanation

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Find Thevenin’s and Norton’s Equivalent Circuits