Find 
using superposition rule:
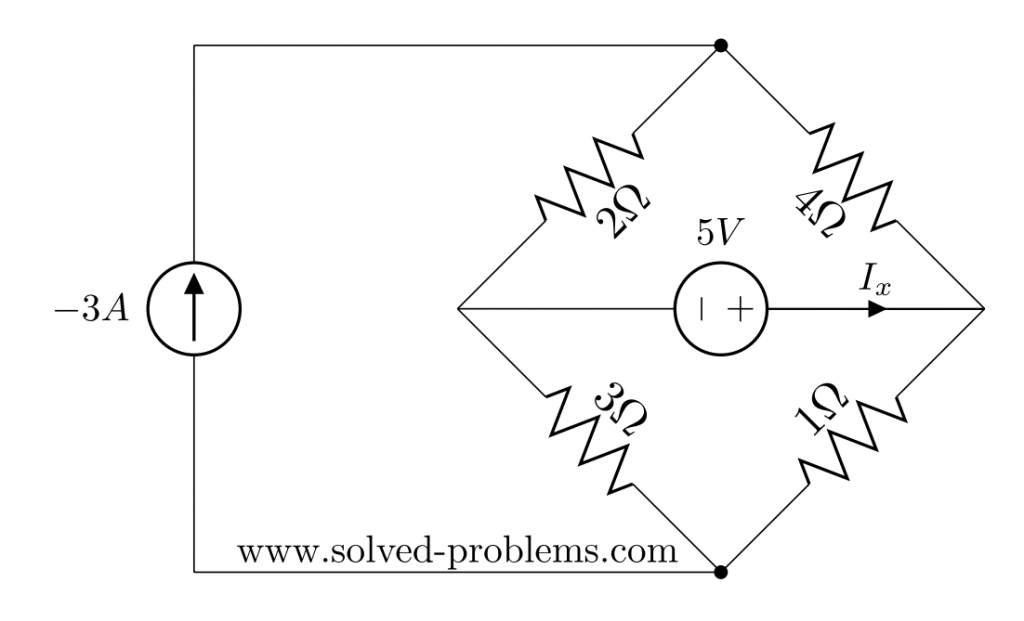
Solution
Superposition
The superposition theorem states that the response (voltage or current) in any branch of a linear circuit which has more than one independent source equals the algebraic sum of the responses caused by each independent source acting alone, while all other independent sources are turned off (made zero).
There are two sources, so we need to turn them off one by one and calculate associated values.
Two announcements before we start! First, a PDF sheet of this problem with the solution and side space for notes can be downloaded below. Second, you may watch solving this problem on the video posted below. My suggestion is that you print the solution sheet and make notes on it while watching the video. Please subscribe to my YouTube channel for more videos!
Let’s start with the current source. To turn a current source off we need to replace it with an open circuit. Easiest way to remember this is that to turn off a source we must make its value zero and for a current source we need to make its current zero. Zero current means no way for current to pass and that is possible with an open circuit.
Or simply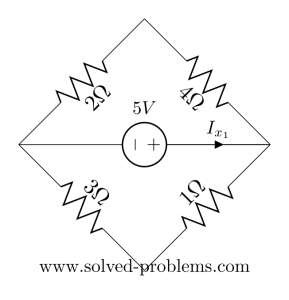
and 
are in series and also 
and 
:
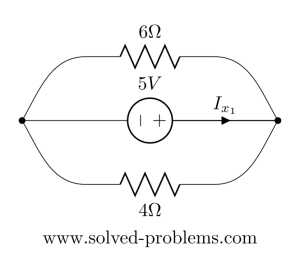
Now and 
are parallel:
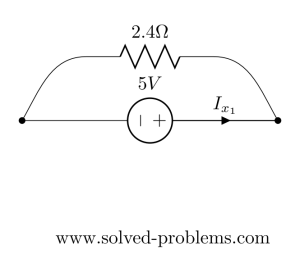
So using Ohm’s law:
To continue solving the circuit with the Superposition method, we should make the voltage source zero and find the contribution of the current source on 
. Making voltage source means replacing it with a short circuit. Similar to the current source, you may memorize this by remembering that you need to make the source value (here: voltage) equal to zero and to force zero voltage drop between two points you need to connect them.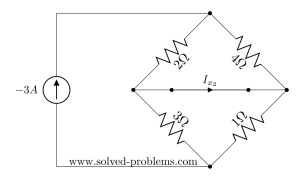
For a moment forget and concentrate on finding current of resistors. If we have the current of resistors, we can easily apply KCL and find 
. So, and are parallel and also and are parallel:
Now, we can find their voltage drops:
Please note that the voltage drop on 
is the same as and voltage drops, because the circuits are equivalent and all are connected to the same nodes. The same statement is correct for 
voltage drop and and voltage drops. So
To find all we need is to write KCL at one of the nodes: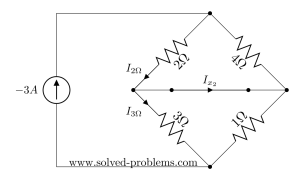
and 
can be found using Ohm’s law:
Therefore,
And
Now, replace resistor with a one and solve the circuit using superposition method. Let me now your answer below in the comments section.
0.33 A
how
but if we use the mesh analysis we will get -2.08 A …
and ix2=-1.25 A
SO ix=-3.33 A
This is a great discovery, I really appreciate your efforts on these solved problems with easy steps to understand.
11/3=3.67
After replacing the resistor, I found the solution of example as Ix1 = 1.388, Ix2 = 0, and therefore Ix has to be 1.388 right?
Let’s see what others found!
I will like to view an example in superposition with three resistors in parallel with to voltage sources in the left resistor and other in the midle resistor to find the current in the right resistor first and in the midle resistor secondly.
0.14 A
I like the example given
Well done, That is great.
I got my final current to be 12.5A?
I followed the same method as aboveand got 18A for the current from the first circuit and -6.5A for the second circuit, combining i got I=12.5A
11.5lol
Can I see an example of a linear circuit where the superposition theorem doesnt work?
Superposition theorem works for all circuits. Of course, there should be more than one independent source to use the superposition.
Sometimes we do not use the superposition simply because using other methods is easier.
Well done
Can i solve this circuit using the other theorem? (Source transformation)
Ix1=1.4A and Ix2=0.01A and Ix=1.41A
2 01 A is answer
Nice explanation 🙂
Keep it up..
Ix1= 1.3888A
Ix2= 0.0000A
Hence Ix = Ix1 + Ix2 = 1.3888A
1.38A
1.38 A for Ix 1 and 0A for so current is 1.38 A
Ans:Ix=2.339amps
When we kept 6ohms instead of 1ohm