Solve the circuit by mesh analysis and find the current and the voltage across .

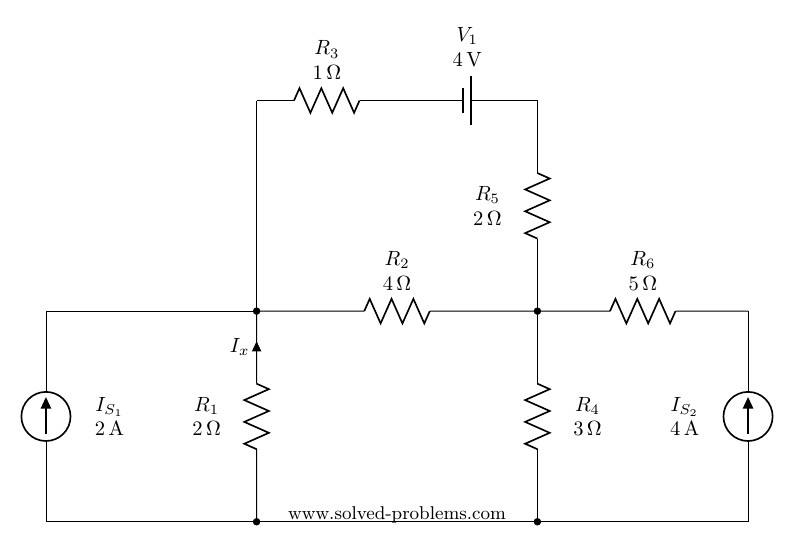
Solution

Mesh Analysis

There are four meshes in the circuit. So, we need to assign four mesh currents. It is better to have all the mesh currents loop in the same direction (usually clockwise) to prevent errors when writing out the equations.

Update 2019/07/27
You may also watch it on YouTube now!

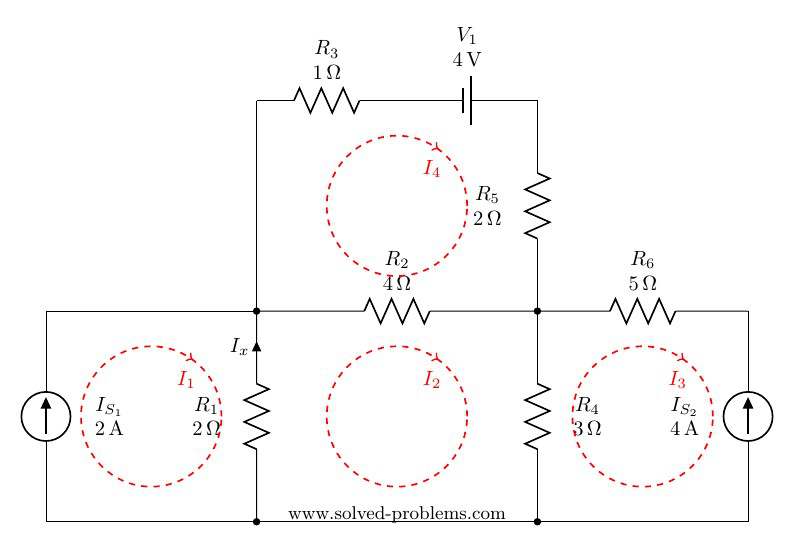
A mesh current is the current passing through elements which are not shared by other loops. This is to say that, for example, the current of is , the current of is and so on. But how about elements shared between two meshes such as ? Current of such elements is the algebraic sum of both meshes. Lets assume that the current of is defined with direction from right to left, algebraic sum means that its current would be . If one assume the inverse direction, i.e. from bottom to top, it would be because is passing through with the same direction of its defined current but is passing with the reverse direction.

Lets define current directions for all elements and find them in terms of mesh currents:

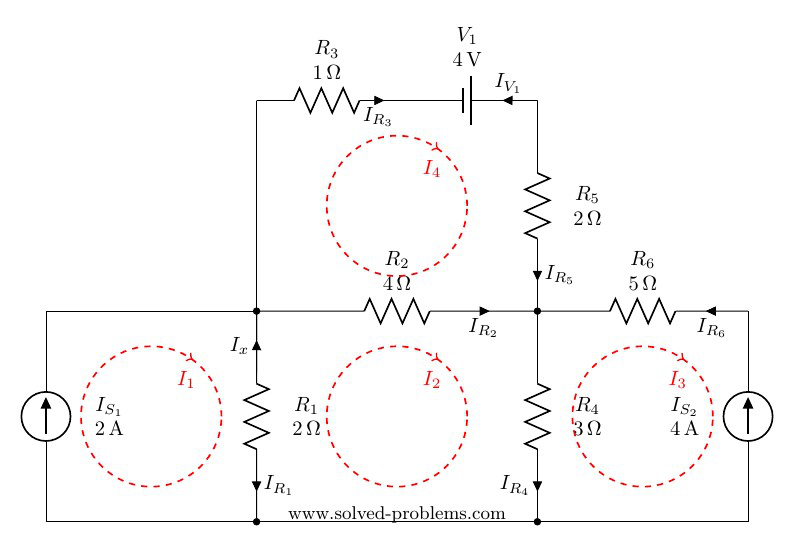
Resistors

is shared between mesh #1 and mesh #2, i.e. meshes with currents and . Therefore equals to the algebraic sum of and . To determine signs of mesh currents for , we need to compare mesh current directions with the direction. It is clear that is in the same direction of and is in the opposite direction. Thus, .

As we discussed earlier, .

is not shared between meshes. It is only in mesh #4 and because is in the same direction of , .

Similar to : .

Similar to : .

It is similar to with one exception; the direction of is opposite to the direction of the mesh current, i.e. . Therefore, .

Voltage Source

Similar to , since the defined current direction is opposite to the mesh current direction: .

Current Sources

Current sources are known but finding their values in term of mesh currents helps to find mesh current values.

It is not shared between any mesh and in the same direction as the mesh current. Thus

It is not shared between any mesh and in the reverse direction of the mesh current. Thus

Known and unknown mesh currents

Current sources, specially when they are not shared between meshes, are very useful in determining mesh current values. SO far we have found:


But and are still unknown.

Now, lets write the equation for mesh of (Mesh II). A mesh equation is in fact a KVL equation using mesh currents. We start from a point and calculate algebraic sum of voltage drops around the loop. We try to avoid introducing more unknowns to equations than the mesh currents. For example, instead of , we use . With some practice, you can easily write KVL equations using mesh currents directly. For resistors, the voltage drop equals to the resistance multiplied by mesh currents considering mesh currents in your KVL writing direction with positive sign and for the ones in the opposite direction with negative sign. Lets assume for mesh 2 we start from left-bottom toward top:

is in the same direction of our KVL and therefore comes with positive sign but is in the opposite direction and comes with negative sign. Similarly:



(1)
For Mesh IV, starting from left-bottom toward top and then right:

This is because is not a shared element.


(2)
Solving equations 1 and 2, we obtain:

Finding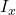

The current of any branch is equal to the algebraic sum of associated mesh currents. is in the opposite direction of and is in the same direction as . Therefore:
.

Finding voltage across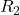

.

When To Use Mesh Analysis?

It depends on the number of meshes in the circuit comparing to the number of nodes. If there are more meshes than nodes, it is usually better to use mesh analysis.

Homework

Solve this circuit using mesh analysis and find and :

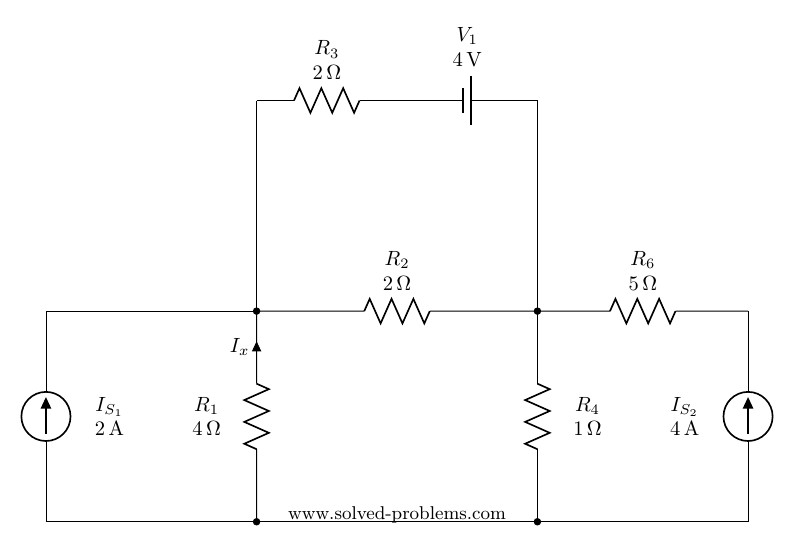
Answers