Solve the circuit with the nodal analysis and determine 
and 
.
Solution
1) Identify all nodes in the circuit. Call the number of nodes 
.
The circuit has 5 nodes. Therefore, 
.
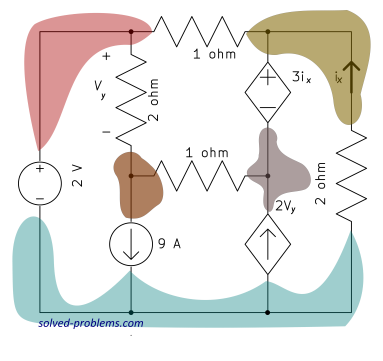
2) Select a reference node. Label it with reference (ground) symbol.
The node at the bottom is the best candidate. It is the node with largest number of elements connected to it.
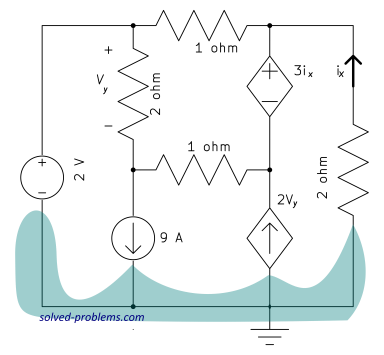
3) Assign a variable for each node whose voltage is unknown.
Four nodes are remaining:
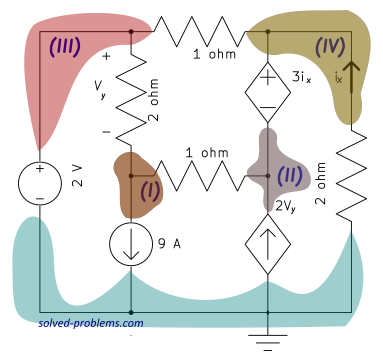
Node I is a regular node. A dependent voltage source is located between node II and node III. Therefore, node II and node III form a supernode. Node IV is connected to a voltage source whose other node is the reference node. We label the voltages of node I and node II with 
and 
respectively.
For node IV, the 
voltage source provides the voltage of the node. Since the positive terminal of the voltage source is connected to the node, the node voltage is 
.
4) If there are dependent sources in the circuit, write down equations that express their values in terms of other node voltages.
The voltage of node III is 
. On the other hand 
is the current of the 
resistor in the right hand side. Using the Ohm’s law:
voltage of the resistor = 
. (Eq. 1)
Please note that the direction of is from the reference node to node III. Since it is always assumed that the reference node is the negative terminal for the defined node voltages, the voltage of node III is 
(instead of 
).
By solving Eq. 1:
.
Consequently, the voltage of node III is 
.
Note that we always write unknowns in terms of node voltages in nodal analysis.
Note that 
. 
is the current of the dependent current source. Now, we need to find the current of the dependent current source in terms of the node voltages. is the voltage across node IV and Node I. The positive terminal is connected to node IV and the negative one is connected to node II. Therefore, 
. You can verify this by applying KVL around the loop consisting of the reference node, node I and node IV.
5) Write down a KCL equation for each node by setting the total current flowing out of the node to zero.
For node I:
.
(Eq. 2)
For supernode II&III:
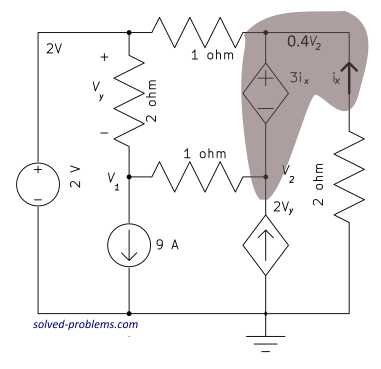
. Substituting and simplifying:
. (Eq. 3)
Solving the set of equations Eq. 2 and Eq. 3 results in 
and 
. Therefore 
and 
.
Good Job!! You should be a teacher in my University.
The nodes you labelled in step 3 don’t correspond to what you’re writing later, unless I’ve misunderstood the labeling. Don’t node II and node IV form the supernode, and not node II and III? Also, I don’t see how node IV is connected to the 2V source? That would be node III wouldn’t it?
You are right.
IIIII and IV must be swapped in the step 3 picture. Thank you.I think you would swap III and IV? Since you say that there is a dependent source located between nodes II and IV.
I mean dependent source between nodes II and III*.
I also don’t understand how you got V2+3ix=V2-(3/5)V2=0.4V2 for the node voltage in step 4.
$latex V_2=-5i_x \to i_x=-\frac{1}{5}V_2$
Substituting this in $latex V_2+3i_x$ gives $latex V_2+3i_x=\frac{2}{5}V_2=0.4V_2$
i think u had accidentally labelled wrongly the 3rd and 4th node…then , why u did not consider the 1 ohm resistor at th 3rd node ?
Well, it is not used in equations. This does not mean that it is missed somewhere. So, the solution and answers are correct. If you check you will see that the current of that resistor is zero so its value is not important, the answers would not change if its replaced with short circuit or open circuit, ….
Good job…i understood easily by ur description thnx ya
hi,can some one told me about the equition that how we will write equition for a circuit which have a supernode
Hi Ishraq,
Please download my ebook on Nodal Analysis from . Supernode is also covered.
plz solve norton equivalent circuit calculating I-norton and R-noton having
1) no independent source and dependent voltage source
2) no independent source and dependent curent source
3)1 independent source and 1 dependent souce
Sure. I will add some solved problems for Norton equivalent soon.
i’m stupid and you omitted too much information in your derivations for someone with my brain to understand how you arrived at certain equations.
“A dependent voltage source is located between node II and node III. Therefore, node II and node III form a supernode. Node IV is connected to a voltage source whose other node is the reference node. ”
Hi again. I think that you must interchange the names between nodes 3 and 4. You have to name node 4 as node 3 and node 3 as node 4. Please, check it.
How about showing us a cccs on the perimeter of a circuit , the cccs having no resistors across it nor any voltage sources across it?