Determine the power of each source after solving the circuit by the nodal analysis.

I. Identify all nodes in the circuit.
The circuit has 6 nodes as indicated below:

II. Select a reference node. Label this node with the reference (ground) symbol.
The bottom left node is connected to 4 nodes while the other ones are connected to three or less elements. Therefore, we select it as the reference node of the circuit.

III. Assign variables for unknown node voltages.
We label the remaining nodes as shown above. ![]() is connected to the reference node through a voltage source. Therefore, it is equal to the voltage of the voltage source:
is connected to the reference node through a voltage source. Therefore, it is equal to the voltage of the voltage source: ![]() .
.
IV. Incorporate dependent sources. There are no dependent sources in this circuit.
V. Apply Kirchhoff’s Current Law (KCL) / VI. Handle super-nodes.
Nodes of ![]() and
and ![]() are connected by a voltage source. Therefore, they form a super-node. The negative terminal of the voltage source is connected to
are connected by a voltage source. Therefore, they form a super-node. The negative terminal of the voltage source is connected to ![]() and the positive terminal is connected to
and the positive terminal is connected to ![]() . Thus,
. Thus,
![]()
This can also be verified by a KVL around the loop which starts from the reference node, jumps to the node of ![]() with
with ![]() (the reference is always assumed to be the negative terminal of node voltages), passes through the voltage source by
(the reference is always assumed to be the negative terminal of node voltages), passes through the voltage source by ![]() and returns back to the reference node from
and returns back to the reference node from ![]() as
as ![]()
![]()
Super-node of ![]() &
& ![]() :
:
![]()
![]()
![]()
![]()
![]()
Node of ![]() :
:
![]()
![]()
![]()
Node of ![]() :
:
![]()
![]()
![]()
![]()
Hence, we have the following system of equations:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} 61 V_3-6 V_4-10 V_5=100 \\ -6V_3+11 V_4=-300 \\ -4 V_3+7V_5=128 \end{array} \right.\]](https://www.solved-problems.com/wp-content/ql-cache/quicklatex.com-265860250d9eab754e916d35e60577c6_l3.png)
VII. Solve the System of Equations.
This system of equations can be solved by any preferred method such as elimination, row reduction, Cramer’s rule or other methods. We use the Cramer’s rule here:

![]()
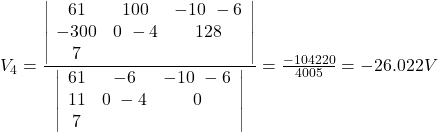
![]()
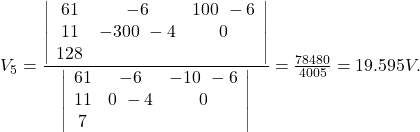
![]()
VIII. Determine Additional Variables.
After solving for all node voltages, we can calculate the currents and powers for the sources in the circuit as follows:
- Current of the
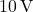 Source:
Source:
The current through the ![]() source is the same as the current through the
source is the same as the current through the ![]() resistor. Using Ohm’s Law, this current is:
resistor. Using Ohm’s Law, this current is:
![]()
The current direction is chosen such that it enters the positive terminal of the voltage source, in compliance with the \textit{passive sign convention}.
The power delivered by the ![]() source is then:
source is then:
![]()
Since the power is negative, the source is \textbf{absorbing power}.
- Current of the
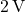 Source:
Source:
The current through the ![]() source is the sum of the currents through the
source is the sum of the currents through the ![]() and
and ![]() resistors. Using Ohm’s Law, we calculate:
resistors. Using Ohm’s Law, we calculate:
![]()
Substituting the values:
![]()
The power delivered by the ![]() source is:
source is:
![]()
Since the power is positive, the source is supplying power.
- Voltage Across the
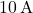 Current Source:
Current Source:
The voltage across the ![]() current source is given by the difference in node voltages:
current source is given by the difference in node voltages:
![]()
The power delivered by the ![]() source is:
source is:
![]()
Since the power is negative, the source is \textbf{supplying power}.
Download the Circuit File
To download the LTspice circuit file for your own simulations, click the link below.Please remember to unzip the file after downloading to access the .asc file for your simulations:

Leave a Reply