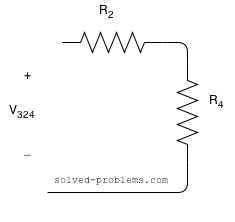
Determine voltage across ![]() and
and ![]() using voltage division rule.
using voltage division rule.
Assume that
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
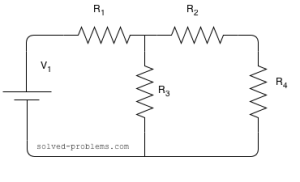
Solution:
Please note that the voltage division rule cannot be directly applied. This is to say that:
![]()
The reason is that some current of ![]() is passing through
is passing through ![]() and
and ![]() branch. If the branch was broken at some point, for example as:
branch. If the branch was broken at some point, for example as:
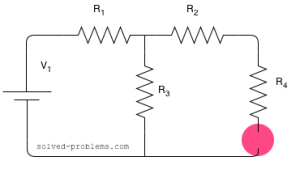
we could apply the voltage division rule and say
![]()
But for the original circuit, the equation above is not correct. To solve the circuit using the voltage divider, we have to find the Thevenin equivalent of the colored circuit:
![]() and
and ![]() are in series and their equivalent equals
are in series and their equivalent equals ![]()
![]() and
and ![]() are parallel and their equivalent equals
are parallel and their equivalent equals ![]()
So, the circuit is simplified to this level now:
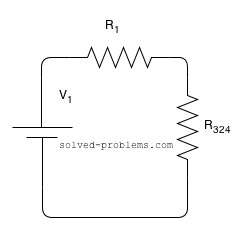
And the voltage division rule can be applied directly:
![]()
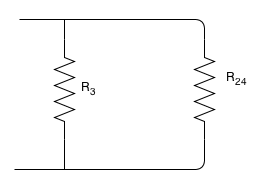
Please note that ![]() is the voltage across
is the voltage across ![]() and the series combination of
and the series combination of ![]() and
and ![]() as shown below:
as shown below:

Now, we can use the voltage division rule to find ![]() and
and ![]() . We can ignore the rest of the circuit and assume that this portion is as:
. We can ignore the rest of the circuit and assume that this portion is as:
![]()
Leave a Reply