Mesh Analysis – Supermesh

Solve the circuit and find the power of sources:

, , , , , .

Solution:
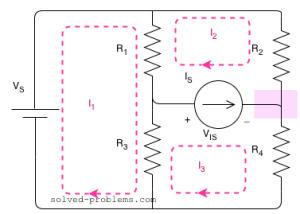
There are three meshes in the circuit. So, we need to assign three mesh currents. It is better to have all the mesh currents loop in the same direction (usually clockwise) to prevent errors when writing out the equations.


A mesh current is the current passing through elements which are not shared by other loops. This is to say that for example the current of the voltage source is , the current of is and so on. But how about elements shared between two meshes? Current of such elements is the algebraic sum of both meshes. For example if we assume the current of is defined with direction from top to bottom, its current would be . If one assume the inverse direction, i.e. from bottom to top, it would be .
Now, lets write the equation for mesh of (Mesh I). A mesh equation is in fact a KVL equation using mesh currents. We start from a point and calculate algebraic sum of voltage drops around the loop:
First the voltage source:

Now we have reached from its upper node. So its current is and we have:

One important point that you should remember and it always help you to validate the equation is that the current part for resistors is always equal to the current of the mesh that we are writing the equation for minus the current of the other mesh. Of course this is only valid if you respect the convention to

• define all the mesh currents in the same direction
• go around the loop at the same direction as the mesh current that you defined while writing the equation

Let’s continue writing the equation. The next element, which is also the last element, is . Without further thinking we can say that the term associated with this element is . (Why?)
.
The equation for Mesh I is done. The next mesh is Mesh II. But wait! what is the voltage across the current source to write in the mesh KVL equation? We don’t know. There are two ways to resolve this issue:

• Assign a voltage to the current source (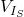). Write equations using 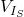and later add equations of Mesh II and III to get rid of .
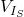• Write the equation for the Supermesh II & III.

A supermesh is a larger loop which has both meshes inside.
Let’s try both methods.
1) Using

Mesh II:

Note that for , unlike the equation for Mesh I, the current is . This is because we are walking around the loop with the direction of , or briefly it is because we are writing the equation for mesh of .

Mesh III:
.

Let’s add two equations:

Simplifying:

2) Supermesh
Here is the supermesh:

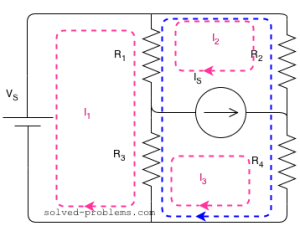
Around the loop clockwise:
.
As you can see, we were able to write the equation in one shot. That is why the supermesh method is preferred.

Now, we have two equations: one for Mesh I and one for the supermesh. But there are three unknowns: , and . So we need another equation. The third equation comes from the current source by writing KCL one of its nodes. We choose the node which is not shared by third loop which is the loop at the right hand side for this example. This way we minimize the number of terms in the equation. Note that the current of and are and , respectively, but the terms for and are more complicated because of involvement.
Let’s apply KCL for the right hand side node. and are entering to the node and is leaving.

Now we have all three equations:

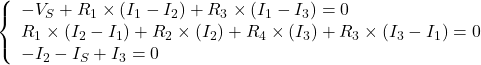
Let’s substitute values:
, , , , , .


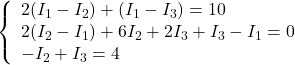
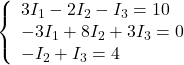
4.9166


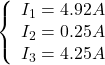
The circuit is solved. Any other voltage or current in the circuit can be easily found using mesh currents. To find power of sources, we need current of the voltage source and voltage across the current source.
For the voltage source, current is equal to as it is located at the unshared part of Mesh I. The current is entering from the negative terminal. Therefore, the active sign convention should be used to find the sign of power:
(supplying power).
Take a look here if you are would like to know how power of independent sources should be calculated.

For the current source, the voltage is and can be calculated by KVL equation of mesh II:

Here, the current is entering from the positive terminal. So, the passive sign convention should be used:
(supplying power).

Now, it is on you to find the power of all resistors and validate that the power conservation law is satisfied.