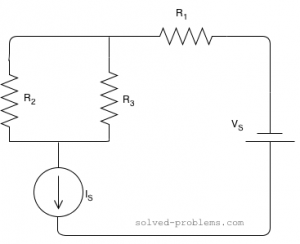
Find current of resistors, use the current division rule.
Problem 1246 (1)
Suppose that R_1=2 \Omega, R_2=4 \Omega, R_3=1 \Omega, I_S=5 A and V_S=4 V

Solution:
R_2 and R_3 are parallel. The current of I_S is passing through them and it is actually divided between them. The branch with lower resistance has higher current because electrons can pass through that easier than the other branch. Using the current division rule, we get

I_{R_2}=\frac{R_3}{R_2+R_3} \times I_S= \frac{1}{1+4} \times 5= 1 A
I_{R_3}=\frac{R_2}{R_2+R_3} \times I_S= \frac{4}{1+4} \times 5= 4 A.
Note that I_{R_2}<I_{R_3} because R_2>R_3.

What is the direction for I_{R_2} and I_{R_3}? It is with the same direction as I_S:
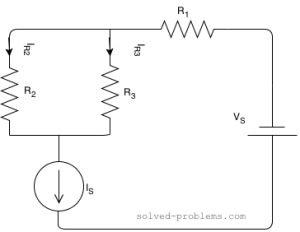
Problem 1246 (2)
We have found I_{R_2} and I_{R_3}, now we need to find I_{R_1}.

If you look at the circuit carefully, R_1, V_S and I_S are all in series. The bottom node of I_S is connected to the bottom node of V_S and there is no other component connected there. And the other node of V_S is connected to R_1, again no other component here. This means that all current of I_S should pass through V_S and the same current must go through R_1. So, the current of R_1 can be easily found:
I_{R_1}=I_S= 5 A.

The direction is the same current as the current source direction:
Problem 1246 (3)
Now, tell me what is the voltage drop across the current source?

Published by Yaz

Hi! Yaz is here. I am passionate about learning and teaching. I try to explain every detail simultaneously with examples to ensure that students will remember them later too.

Join the Conversation

9 Comments

  1. Reply

    1. KCV around the loop assuming the positive terminal of the current source to be the one at bottom:
      +V_{I_S}-R_3 \times I_{R_3}-R_1 \times I_{R_1}-V_S=0

      V_{I_S}=R_3 \times I_{R_3}+R_1 \times I_{R_1}+V_S
      V_{I_S}=1 \times 4+2 \times 5 +4=18 V

      If you label the voltage terminals of the current source the other way, you would get -18 V.
      I think you forgot the voltage source.

      Reply
  2. Reply

  3. Sir please help me .I can’t identify nodes in circuit tell me a wise definition that cover all aspects of node . If you illustrated this with a figure I’ll be thankful.

    Reply
  4. Reply

  5. Sir,why are you not consider the mesh having the parallel combination of(4II1) for the calculation of voltage drop across current Is?

    -Vs-R1*5-(4II1)*5-Vis=0
    -4-2*5-(4\5)*5=Vis
    -4-10-4=Vis
    -18=Vis

    Reply
  6. Reply

  7. Hi please help , the current divider rule is challenging me , I don’t know which resistors to take and make use of them if asked to determine the current passing through a certain resistor , how do I derive the current divider formula without actually referring ?

    Reply
  8. Reply

Leave a comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.