Determine ![]() ,
, ![]() and
and ![]() using the superposition method.
using the superposition method.

Solution
I. Contribution of the ![]() voltage source:
voltage source:
We need to turn off the current source by replacing it with an open circuit. Recall that we do not turn off dependent sources. The resulting circuit is shown below.

In the left hand side loop, we have
![]()
and in the right hand loop, it is trivial that
![]() .
.
Therefore, ![]() . Applying KVL around the inner loop,
. Applying KVL around the inner loop,
![]()
Substituting ![]() , we have
, we have
![]() .
.
II. Contribution of the ![]() current source:
current source:
The independent voltage source must be replaced with a short circuit as shown below.

The ![]() resistor is parallel with the dependent voltage source, Therefore,
resistor is parallel with the dependent voltage source, Therefore, ![]() and since
and since ![]() , we have
, we have ![]() . Applying KCL at the right bottom node,
. Applying KCL at the right bottom node, ![]() . So,
. So,
![]()
Applying KVL around the inner loop,
![]()
III. The final result
![]()
![]()
![]()
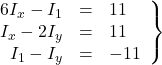
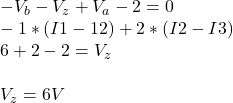
Leave a Reply